Seeing Implicit Neural Representations as Fourier Series
Paper and Code
Sep 01, 2021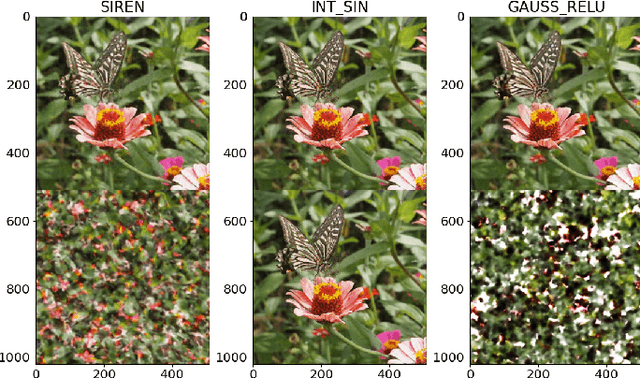
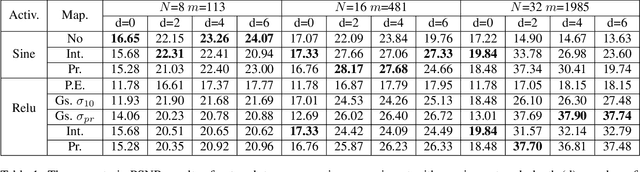

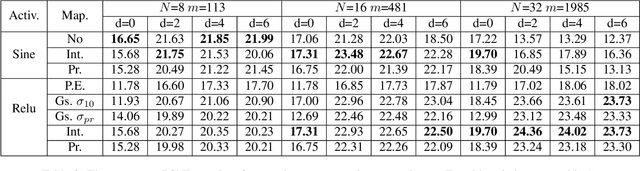
Implicit Neural Representations (INR) use multilayer perceptrons to represent high-frequency functions in low-dimensional problem domains. Recently these representations achieved state-of-the-art results on tasks related to complex 3D objects and scenes. A core problem is the representation of highly detailed signals, which is tackled using networks with periodic activation functions (SIRENs) or applying Fourier mappings to the input. This work analyzes the connection between the two methods and shows that a Fourier mapped perceptron is structurally like one hidden layer SIREN. Furthermore, we identify the relationship between the previously proposed Fourier mapping and the general d-dimensional Fourier series, leading to an integer lattice mapping. Moreover, we modify a progressive training strategy to work on arbitrary Fourier mappings and show that it improves the generalization of the interpolation task. Lastly, we compare the different mappings on the image regression and novel view synthesis tasks. We confirm the previous finding that the main contributor to the mapping performance is the size of the embedding and standard deviation of its elements.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge