SecureFedYJ: a safe feature Gaussianization protocol for Federated Learning
Paper and Code
Oct 04, 2022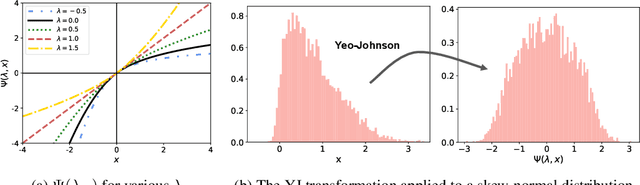

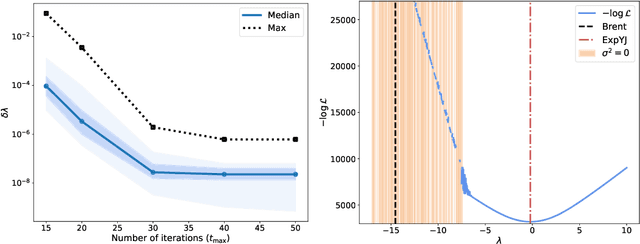
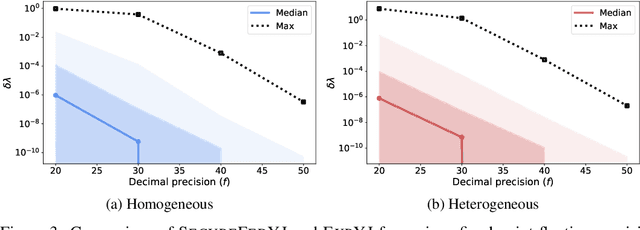
The Yeo-Johnson (YJ) transformation is a standard parametrized per-feature unidimensional transformation often used to Gaussianize features in machine learning. In this paper, we investigate the problem of applying the YJ transformation in a cross-silo Federated Learning setting under privacy constraints. For the first time, we prove that the YJ negative log-likelihood is in fact convex, which allows us to optimize it with exponential search. We numerically show that the resulting algorithm is more stable than the state-of-the-art approach based on the Brent minimization method. Building on this simple algorithm and Secure Multiparty Computation routines, we propose SecureFedYJ, a federated algorithm that performs a pooled-equivalent YJ transformation without leaking more information than the final fitted parameters do. Quantitative experiments on real data demonstrate that, in addition to being secure, our approach reliably normalizes features across silos as well as if data were pooled, making it a viable approach for safe federated feature Gaussianization.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge