Second-order Democratic Aggregation
Paper and Code
Aug 22, 2018
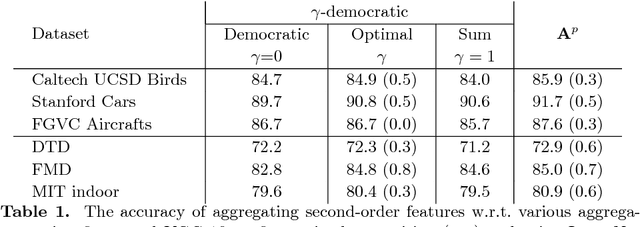
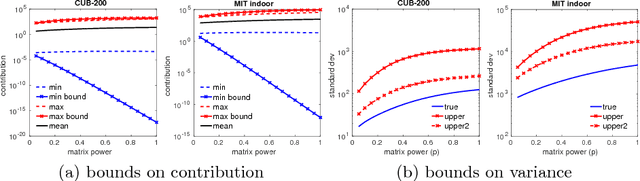

Aggregated second-order features extracted from deep convolutional networks have been shown to be effective for texture generation, fine-grained recognition, material classification, and scene understanding. In this paper, we study a class of orderless aggregation functions designed to minimize interference or equalize contributions in the context of second-order features and we show that they can be computed just as efficiently as their first-order counterparts and they have favorable properties over aggregation by summation. Another line of work has shown that matrix power normalization after aggregation can significantly improve the generalization of second-order representations. We show that matrix power normalization implicitly equalizes contributions during aggregation thus establishing a connection between matrix normalization techniques and prior work on minimizing interference. Based on the analysis we present {\gamma}-democratic aggregators that interpolate between sum ({\gamma}=1) and democratic pooling ({\gamma}=0) outperforming both on several classification tasks. Moreover, unlike power normalization, the {\gamma}-democratic aggregations can be computed in a low dimensional space by sketching that allows the use of very high-dimensional second-order features. This results in a state-of-the-art performance on several datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge