Scaling Up Exact Neural Network Compression by ReLU Stability

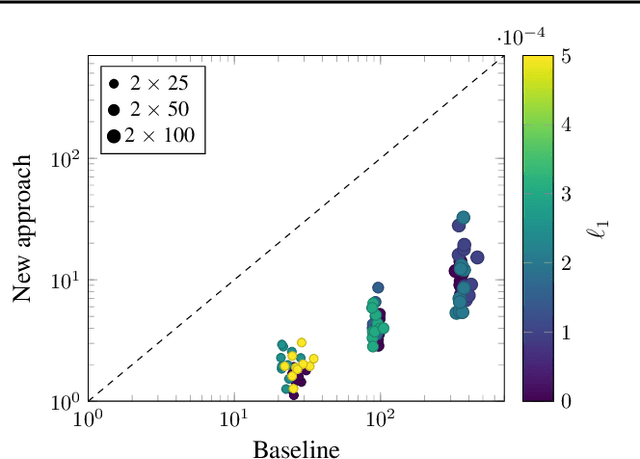
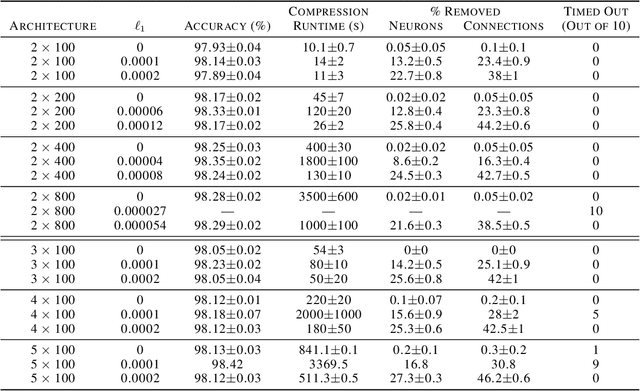
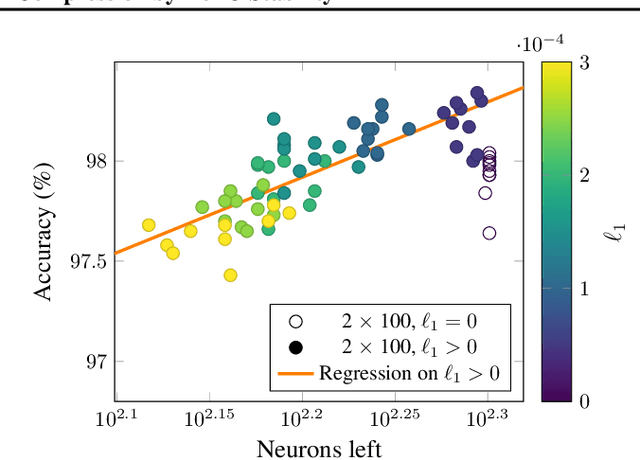
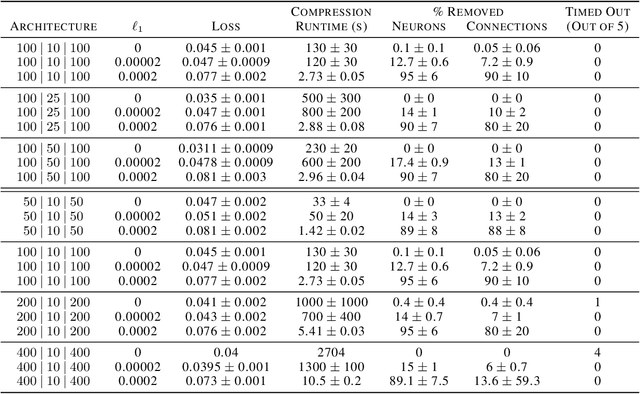
We can compress a neural network while exactly preserving its underlying functionality with respect to a given input domain if some of its neurons are stable. However, current approaches to determine the stability of neurons in networks with Rectified Linear Unit (ReLU) activations require solving or finding a good approximation to multiple discrete optimization problems. In this work, we introduce an algorithm based on solving a single optimization problem to identify all stable neurons. Our approach is on median 21 times faster than the state-of-art method, which allows us to explore exact compression on deeper (5 x 100) and wider (2 x 800) networks within minutes. For classifiers trained under an amount of L1 regularization that does not worsen accuracy, we can remove up to 40% of the connections.