Scale Mixtures of Neural Network Gaussian Processes
Paper and Code
Jul 03, 2021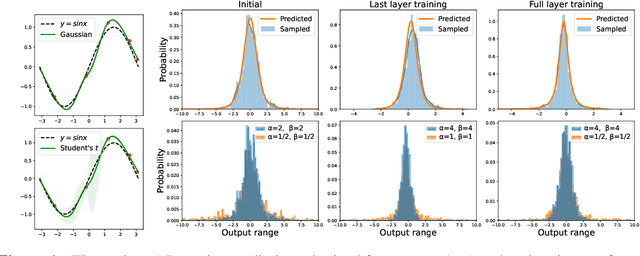
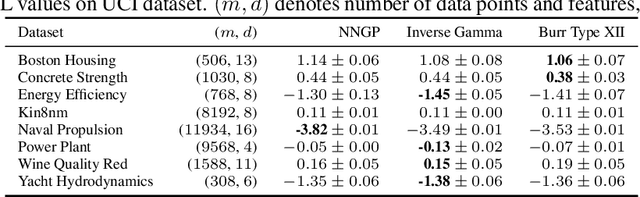
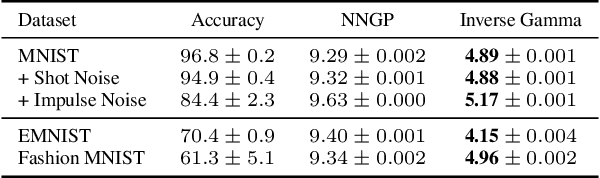
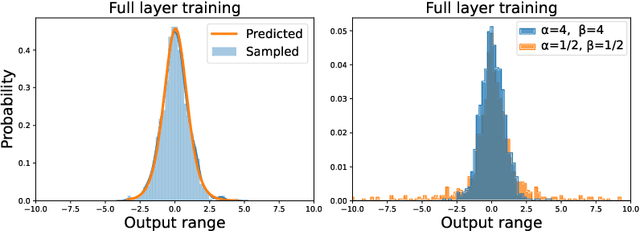
Recent works have revealed that infinitely-wide feed-forward or recurrent neural networks of any architecture correspond to Gaussian processes referred to as $\mathrm{NNGP}$. While these works have extended the class of neural networks converging to Gaussian processes significantly, however, there has been little focus on broadening the class of stochastic processes that such neural networks converge to. In this work, inspired by the scale mixture of Gaussian random variables, we propose the scale mixture of $\mathrm{NNGP}$ for which we introduce a prior distribution on the scale of the last-layer parameters. We show that simply introducing a scale prior on the last-layer parameters can turn infinitely-wide neural networks of any architecture into a richer class of stochastic processes. Especially, with certain scale priors, we obtain heavy-tailed stochastic processes, and we recover Student's $t$ processes in the case of inverse gamma priors. We further analyze the distributions of the neural networks initialized with our prior setting and trained with gradient descents and obtain similar results as for $\mathrm{NNGP}$. We present a practical posterior-inference algorithm for the scale mixture of $\mathrm{NNGP}$ and empirically demonstrate its usefulness on regression and classification tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge