Scalable Sparse Subspace Clustering via Ordered Weighted $\ell_1$ Regression
Paper and Code
Jul 10, 2018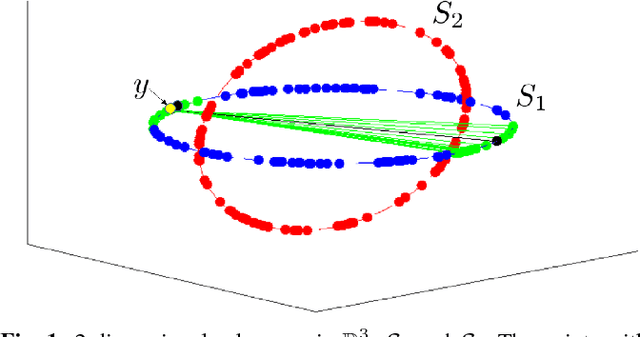

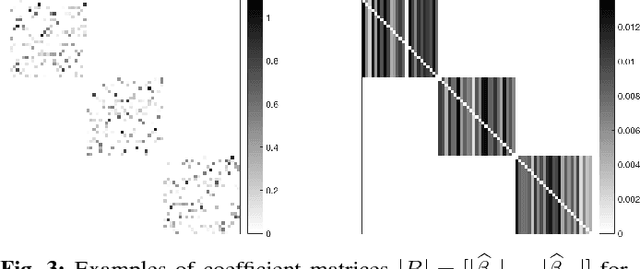

The main contribution of the paper is a new approach to subspace clustering that is significantly more computationally efficient and scalable than existing state-of-the-art methods. The central idea is to modify the regression technique in sparse subspace clustering (SSC) by replacing the $\ell_1$ minimization with a generalization called Ordered Weighted $\ell_1$ (OWL) minimization which performs simultaneous regression and clustering of correlated variables. Using random geometric graph theory, we prove that OWL regression selects more points within each subspace, resulting in better clustering results. This allows for accurate subspace clustering based on regression solutions for only a small subset of the total dataset, significantly reducing the computational complexity compared to SSC. In experiments, we find that our OWL approach can achieve a speedup of 20$\times$ to 30$\times$ for synthetic problems and 4$\times$ to 8$\times$ on real data problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge