Scalable Graph Convolutional Network Training on Distributed-Memory Systems
Paper and Code
Dec 13, 2022
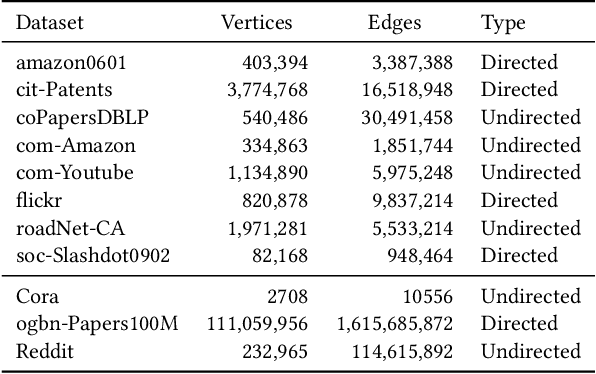
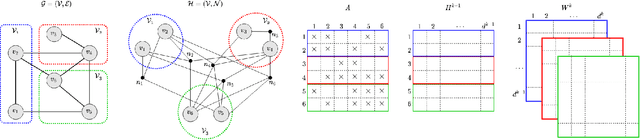
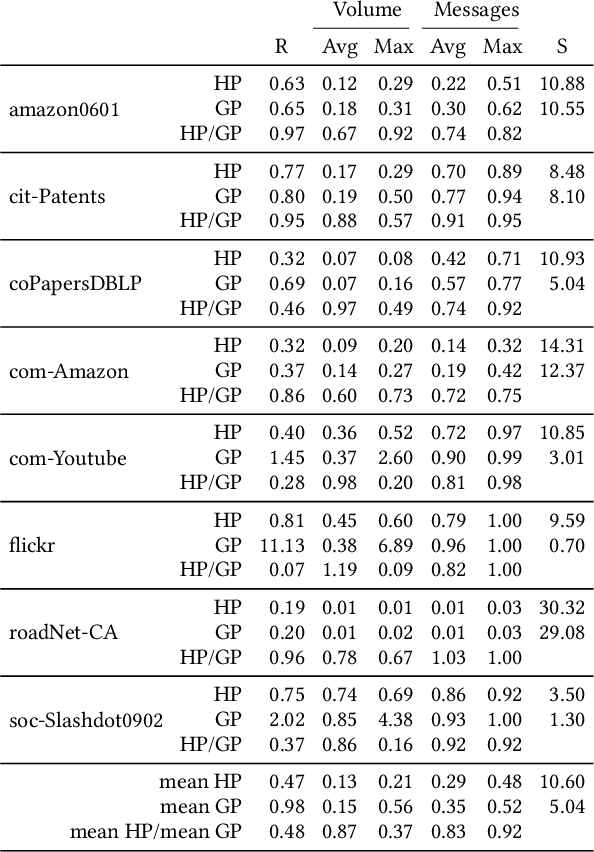
Graph Convolutional Networks (GCNs) are extensively utilized for deep learning on graphs. The large data sizes of graphs and their vertex features make scalable training algorithms and distributed memory systems necessary. Since the convolution operation on graphs induces irregular memory access patterns, designing a memory- and communication-efficient parallel algorithm for GCN training poses unique challenges. We propose a highly parallel training algorithm that scales to large processor counts. In our solution, the large adjacency and vertex-feature matrices are partitioned among processors. We exploit the vertex-partitioning of the graph to use non-blocking point-to-point communication operations between processors for better scalability. To further minimize the parallelization overheads, we introduce a sparse matrix partitioning scheme based on a hypergraph partitioning model for full-batch training. We also propose a novel stochastic hypergraph model to encode the expected communication volume in mini-batch training. We show the merits of the hypergraph model, previously unexplored for GCN training, over the standard graph partitioning model which does not accurately encode the communication costs. Experiments performed on real-world graph datasets demonstrate that the proposed algorithms achieve considerable speedups over alternative solutions. The optimizations achieved on communication costs become even more pronounced at high scalability with many processors. The performance benefits are preserved in deeper GCNs having more layers as well as on billion-scale graphs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge