Scalable Computations of Wasserstein Barycenter via Input Convex Neural Networks

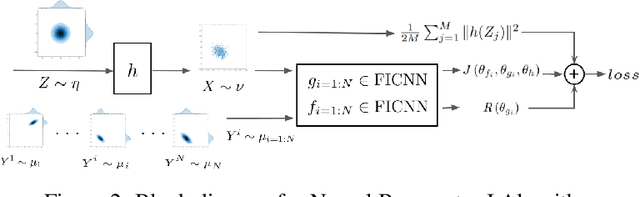
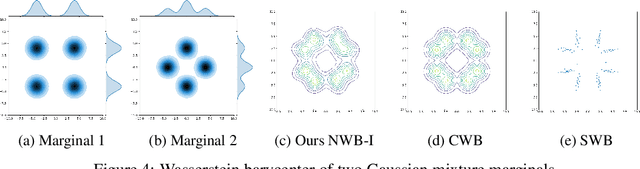
Wasserstein Barycenter is a principled approach to represent the weighted mean of a given set of probability distributions, utilizing the geometry induced by optimal transport. In this work, we present a novel scalable algorithm to approximate the Wasserstein Barycenters aiming at high-dimensional applications in machine learning. Our proposed algorithm is based on the Kantorovich dual formulation of the 2-Wasserstein distance as well as a recent neural network architecture, input convex neural network, that is known to parametrize convex functions. The distinguishing features of our method are: i) it only requires samples from the marginal distributions; ii) unlike the existing semi-discrete approaches, it represents the Barycenter with a generative model; iii) it allows to compute the barycenter with arbitrary weights after one training session. We demonstrate the efficacy of our algorithm by comparing it with the state-of-art methods in multiple experiments.