Satisfiability and Synthesis Modulo Oracles
Paper and Code
Jul 28, 2021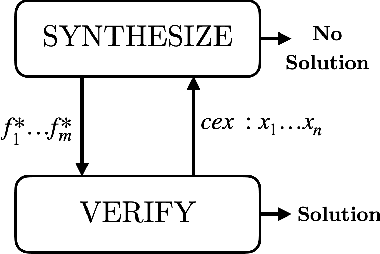
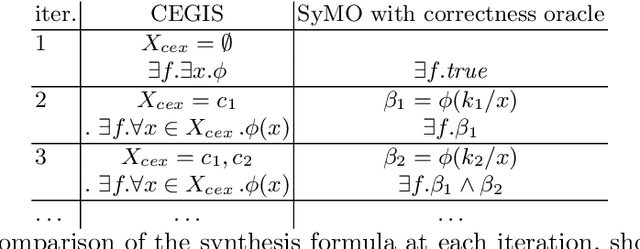


In classic program synthesis algorithms, such as counterexample-guided inductive synthesis (CEGIS), the algorithms alternate between a synthesis phase and an oracle (verification) phase. Many synthesis algorithms use a white-box oracle based on satisfiability modulo theory (SMT) solvers to provide counterexamples. But what if a white-box oracle is either not available or not easy to work with? We present a framework for solving a general class of oracle-guided synthesis problems which we term synthesis modulo oracles. In this setting, oracles may be black boxes with a query-response interface defined by the synthesis problem. As a necessary component of this framework, we also formalize the problem of satisfiability modulo theories and oracles, and present an algorithm for solving this problem. We implement a prototype solver for satisfiability and synthesis modulo oracles and demonstrate that, by using oracles that execute functions not easily modeled in SMT-constraints, such as recursive functions or oracles that incorporate compilation and execution of code, SMTO and SyMO are able to solve problems beyond the abilities of standard SMT and synthesis solvers.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge