Sampling-based Approximations with Quantitative Performance for the Probabilistic Reach-Avoid Problem over General Markov Processes
Paper and Code
Sep 09, 2015

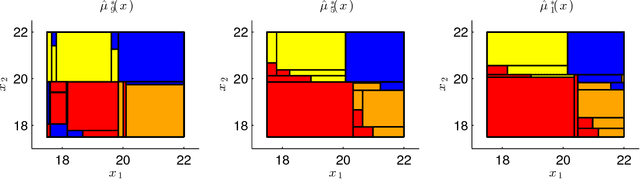

This article deals with stochastic processes endowed with the Markov (memoryless) property and evolving over general (uncountable) state spaces. The models further depend on a non-deterministic quantity in the form of a control input, which can be selected to affect the probabilistic dynamics. We address the computation of maximal reach-avoid specifications, together with the synthesis of the corresponding optimal controllers. The reach-avoid specification deals with assessing the likelihood that any finite-horizon trajectory of the model enters a given goal set, while avoiding a given set of undesired states. This article newly provides an approximate computational scheme for the reach-avoid specification based on the Fitted Value Iteration algorithm, which hinges on random sample extractions, and gives a-priori computable formal probabilistic bounds on the error made by the approximation algorithm: as such, the output of the numerical scheme is quantitatively assessed and thus meaningful for safety-critical applications. Furthermore, we provide tighter probabilistic error bounds that are sample-based. The overall computational scheme is put in relationship with alternative approximation algorithms in the literature, and finally its performance is practically assessed over a benchmark case study.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge