Safe Motion Planning in Unknown Environments: Optimality Benchmarks and Tractable Policies
Paper and Code
Apr 16, 2018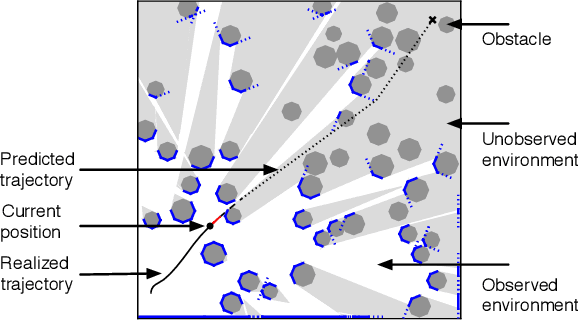
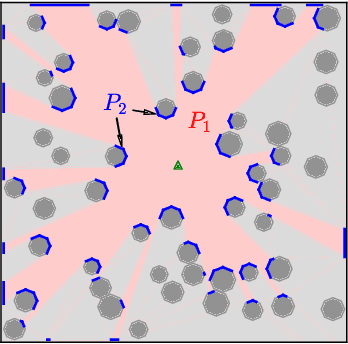
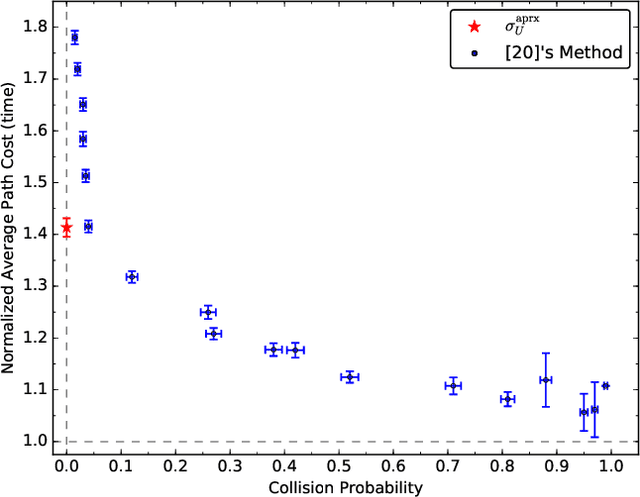
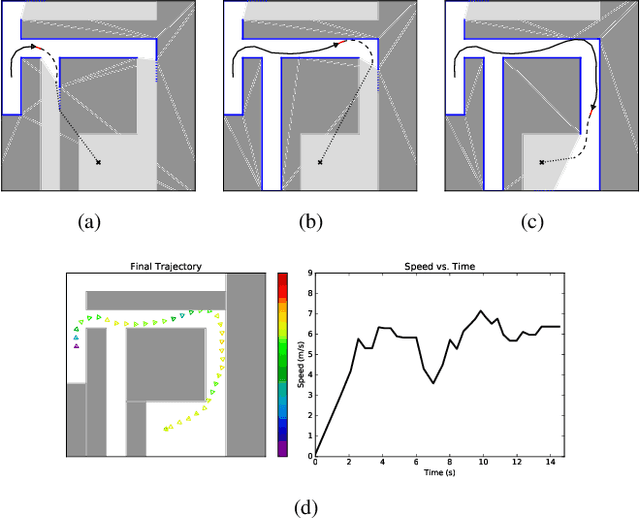
This paper addresses the problem of planning a safe (i.e., collision-free) trajectory from an initial state to a goal region when the obstacle space is a-priori unknown and is incrementally revealed online, e.g., through line-of-sight perception. Despite its ubiquitous nature, this formulation of motion planning has received relatively little theoretical investigation, as opposed to the setup where the environment is assumed known. A fundamental challenge is that, unlike motion planning with known obstacles, it is not even clear what an optimal policy to strive for is. Our contribution is threefold. First, we present a notion of optimality for safe planning in unknown environments in the spirit of comparative (as opposed to competitive) analysis, with the goal of obtaining a benchmark that is, at least conceptually, attainable. Second, by leveraging this theoretical benchmark, we derive a pseudo-optimal class of policies that can seamlessly incorporate any amount of prior or learned information while still guaranteeing the robot never collides. Finally, we demonstrate the practicality of our algorithmic approach in numerical experiments using a range of environment types and dynamics, including a comparison with a state of the art method. A key aspect of our framework is that it automatically and implicitly weighs exploration versus exploitation in a way that is optimal with respect to the information available.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge