Safe Counterfactual Reinforcement Learning

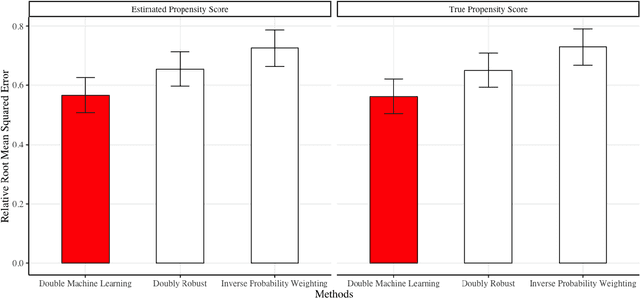
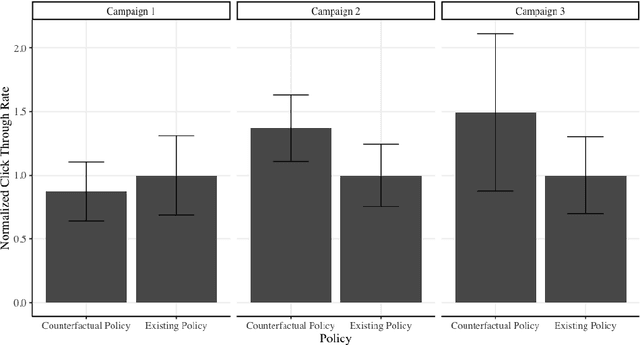
We develop a method for predicting the performance of reinforcement learning and bandit algorithms, given historical data that may have been generated by a different algorithm. Our estimator has the property that its prediction converges in probability to the true performance of a counterfactual algorithm at the fast $\sqrt{N}$ rate, as the sample size $N$ increases. We also show a correct way to estimate the variance of our prediction, thus allowing the analyst to quantify the uncertainty in the prediction. These properties hold even when the analyst does not know which among a large number of potentially important state variables are really important. These theoretical guarantees make our estimator safe to use. We finally apply it to improve advertisement design by a major advertisement company. We find that our method produces smaller mean squared errors than state-of-the-art methods.