SaDe: Learning Models that Provably Satisfy Domain Constraints
Paper and Code
Dec 08, 2021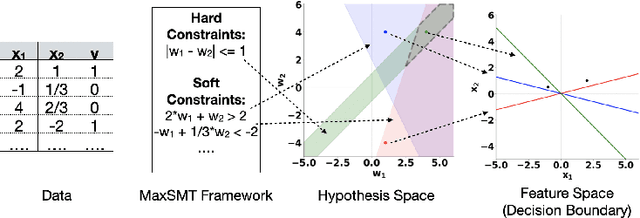

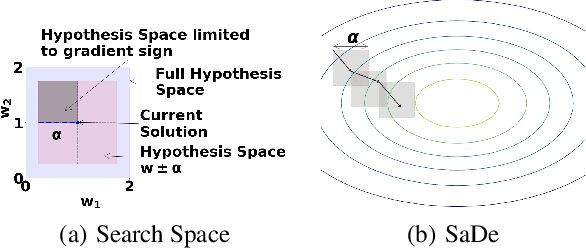
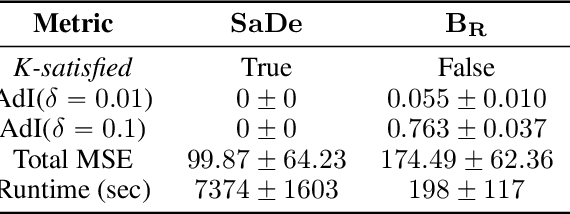
With increasing real world applications of machine learning, models are often required to comply with certain domain based requirements, e.g., safety guarantees in aircraft systems, legal constraints in a loan approval model. A natural way to represent these properties is in the form of constraints. Including such constraints in machine learning is typically done by the means of regularization, which does not guarantee satisfaction of the constraints. In this paper, we present a machine learning approach that can handle a wide variety of constraints, and guarantee that these constraints will be satisfied by the model even on unseen data. We cast machine learning as a maximum satisfiability problem, and solve it using a novel algorithm SaDe which combines constraint satisfaction with gradient descent. We demonstrate on three use cases that this approach learns models that provably satisfy the given constraints.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge