SACBP: Belief Space Planning for Continuous-Time Dynamical Systems via Stochastic Sequential Action Control

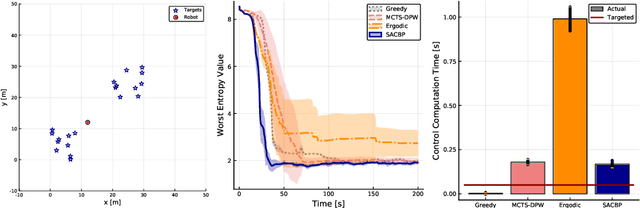
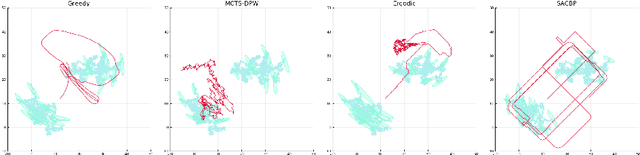
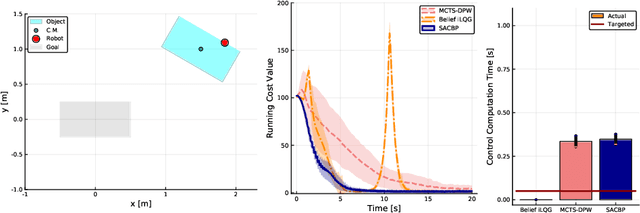
We propose a novel belief space planning technique for continuous dynamics by viewing the belief system as a hybrid dynamical system with time-driven switching. Our approach is based on the perturbation theory of differential equations and extends Sequential Action Control to stochastic belief dynamics. The resulting algorithm, which we name SACBP, does not require discretization of spaces or time and synthesizes control signals in near real-time. SACBP is an anytime algorithm that can handle general parametric Bayesian filters under certain assumptions. We demonstrate the effectiveness of our approach in an active sensing scenario and a model-based Bayesian reinforcement learning problem. In these challenging problems, we show that the algorithm significantly outperforms other existing solution techniques including approximate dynamic programming and local trajectory optimization.