RRT+ : Fast Planning for High-Dimensional Configuration Spaces
Paper and Code
Dec 24, 2016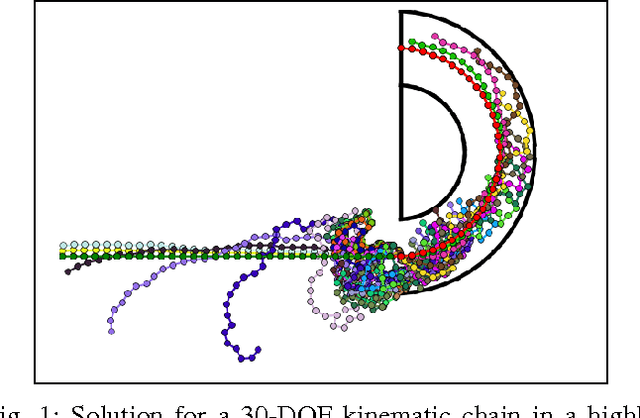
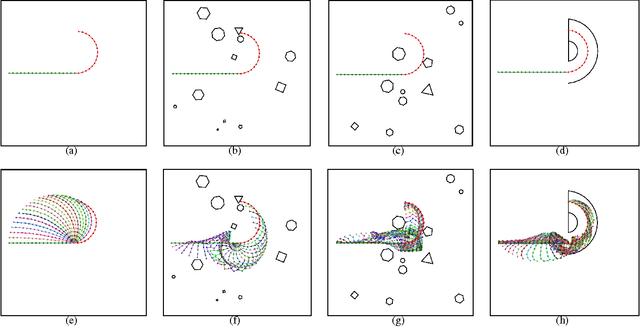
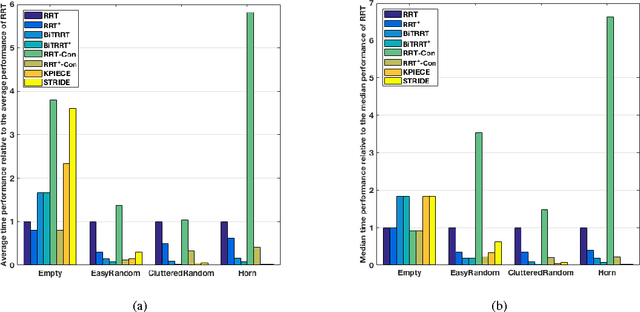
In this paper we propose a new family of RRT based algorithms, named RRT+ , that are able to find faster solutions in high-dimensional configuration spaces compared to other existing RRT variants by finding paths in lower dimensional subspaces of the configuration space. The method can be easily applied to complex hyper-redundant systems and can be adapted by other RRT based planners. We introduce RRT+ and develop some variants, called PrioritizedRRT+ , PrioritizedRRT+-Connect, and PrioritizedBidirectionalT-RRT+ , that use the new sampling technique and we show that our method provides faster results than the corresponding original algorithms. Experiments using the state-of-the-art planners available in OMPL show superior performance of RRT+ for high-dimensional motion planning problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge