Rotation Equivariant 3D Hand Mesh Generation from a Single RGB Image
Paper and Code
Nov 25, 2021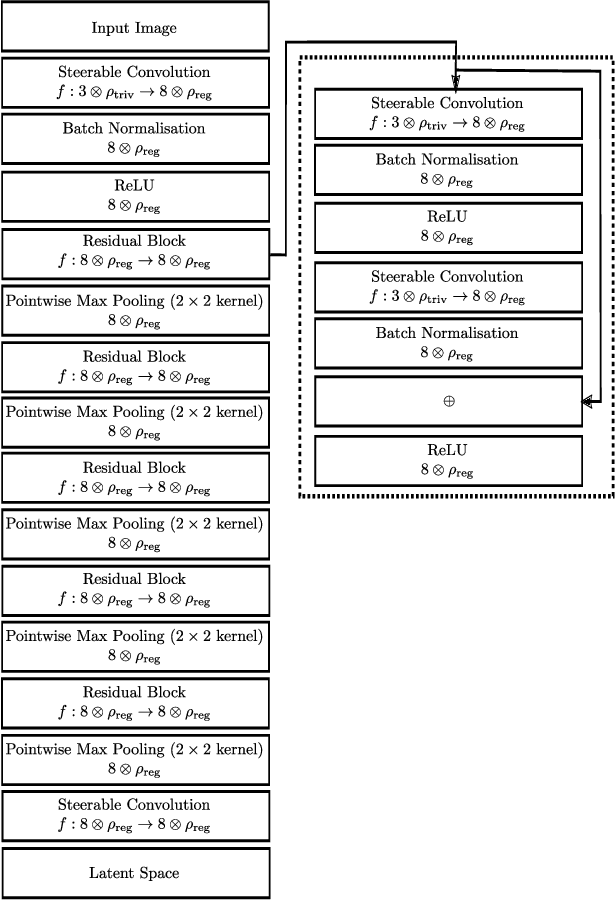
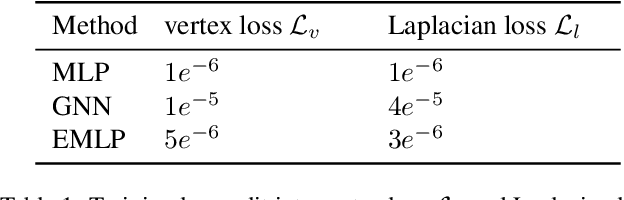
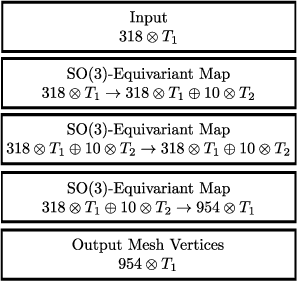
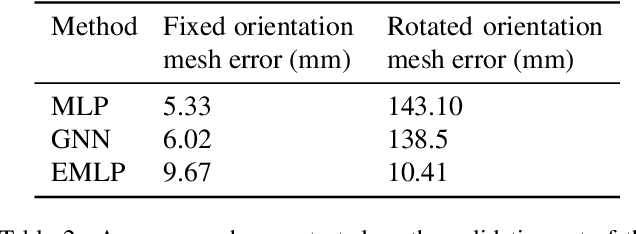
We develop a rotation equivariant model for generating 3D hand meshes from 2D RGB images. This guarantees that as the input image of a hand is rotated the generated mesh undergoes a corresponding rotation. Furthermore, this removes undesirable deformations in the meshes often generated by methods without rotation equivariance. By building a rotation equivariant model, through considering symmetries in the problem, we reduce the need for training on very large datasets to achieve good mesh reconstruction. The encoder takes images defined on $\mathbb{Z}^{2}$ and maps these to latent functions defined on the group $C_{8}$. We introduce a novel vector mapping function to map the function defined on $C_{8}$ to a latent point cloud space defined on the group $\mathrm{SO}(2)$. Further, we introduce a 3D projection function that learns a 3D function from the $\mathrm{SO}(2)$ latent space. Finally, we use an $\mathrm{SO}(3)$ equivariant decoder to ensure rotation equivariance. Our rotation equivariant model outperforms state-of-the-art methods on a real-world dataset and we demonstrate that it accurately captures the shape and pose in the generated meshes under rotation of the input hand.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge