Robustness, Privacy, and Generalization of Adversarial Training
Paper and Code
Dec 25, 2020

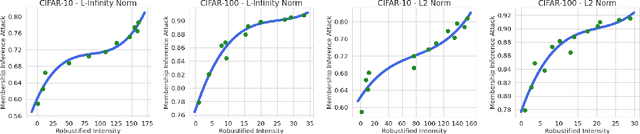
Adversarial training can considerably robustify deep neural networks to resist adversarial attacks. However, some works suggested that adversarial training might comprise the privacy-preserving and generalization abilities. This paper establishes and quantifies the privacy-robustness trade-off and generalization-robustness trade-off in adversarial training from both theoretical and empirical aspects. We first define a notion, {\it robustified intensity} to measure the robustness of an adversarial training algorithm. This measure can be approximate empirically by an asymptotically consistent empirical estimator, {\it empirical robustified intensity}. Based on the robustified intensity, we prove that (1) adversarial training is $(\varepsilon, \delta)$-differentially private, where the magnitude of the differential privacy has a positive correlation with the robustified intensity; and (2) the generalization error of adversarial training can be upper bounded by an $\mathcal O(\sqrt{\log N}/N)$ on-average bound and an $\mathcal O(1/\sqrt{N})$ high-probability bound, both of which have positive correlations with the robustified intensity. Additionally, our generalization bounds do not explicitly rely on the parameter size which would be prohibitively large in deep learning. Systematic experiments on standard datasets, CIFAR-10 and CIFAR-100, are in full agreement with our theories. The source code package is available at \url{https://github.com/fshp971/RPG}.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge