Robustified Time-optimal Point-to-point Motion Planning and Control under Uncertainty
Paper and Code
Jan 24, 2025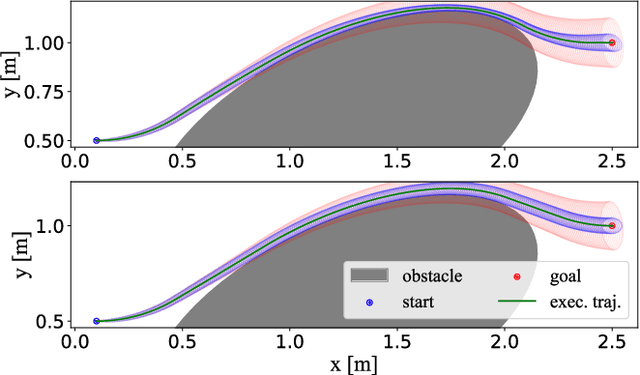
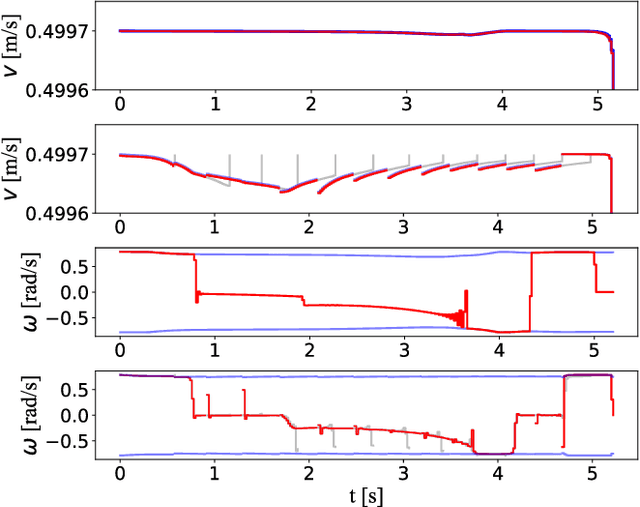
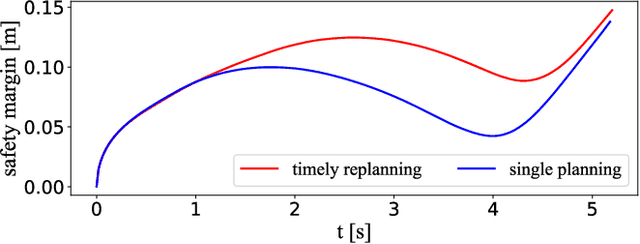
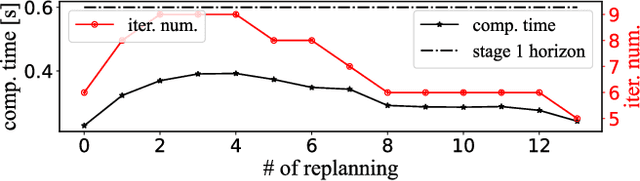
This paper proposes a novel approach to formulate time-optimal point-to-point motion planning and control under uncertainty. The approach defines a robustified two-stage Optimal Control Problem (OCP), in which stage 1, with a fixed time grid, is seamlessly stitched with stage 2, which features a variable time grid. Stage 1 optimizes not only the nominal trajectory, but also feedback gains and corresponding state covariances, which robustify constraints in both stages. The outcome is a minimized uncertainty in stage 1 and a minimized total motion time for stage 2, both contributing to the time optimality and safety of the total motion. A timely replanning strategy is employed to handle changes in constraints and maintain feasibility, while a tailored iterative algorithm is proposed for efficient, real-time OCP execution.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge