Robust Reward Design for Markov Decision Processes
Paper and Code
Jun 07, 2024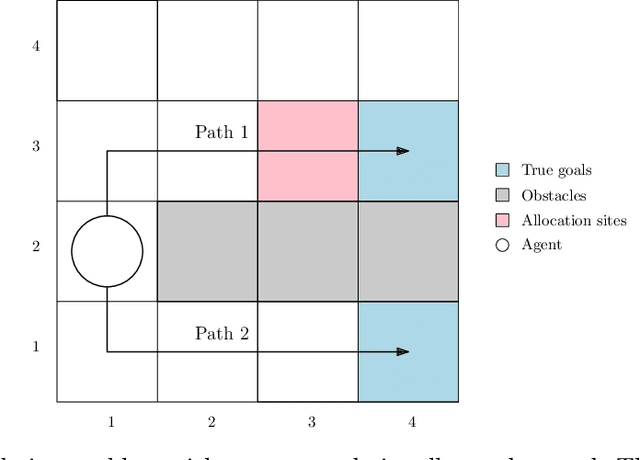

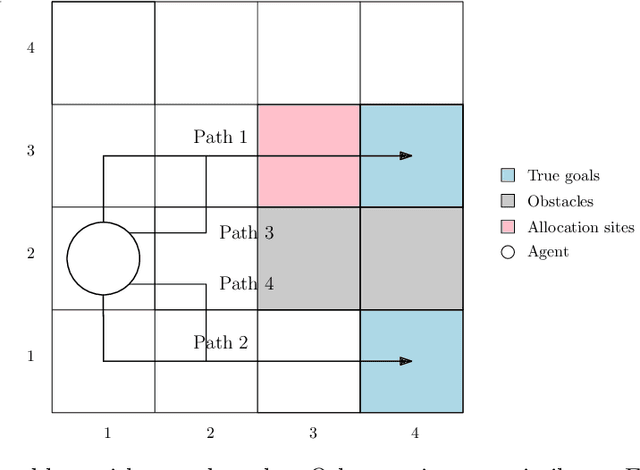
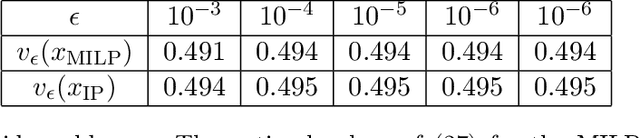
The problem of reward design examines the interaction between a leader and a follower, where the leader aims to shape the follower's behavior to maximize the leader's payoff by modifying the follower's reward function. Current approaches to reward design rely on an accurate model of how the follower responds to reward modifications, which can be sensitive to modeling inaccuracies. To address this issue of sensitivity, we present a solution that offers robustness against uncertainties in modeling the follower, including 1) how the follower breaks ties in the presence of nonunique best responses, 2) inexact knowledge of how the follower perceives reward modifications, and 3) bounded rationality of the follower. Our robust solution is guaranteed to exist under mild conditions and can be obtained numerically by solving a mixed-integer linear program. Numerical experiments on multiple test cases demonstrate that our solution improves robustness compared to the standard approach without incurring significant additional computing costs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge