Robust Offline Reinforcement Learning for Non-Markovian Decision Processes
Paper and Code
Nov 12, 2024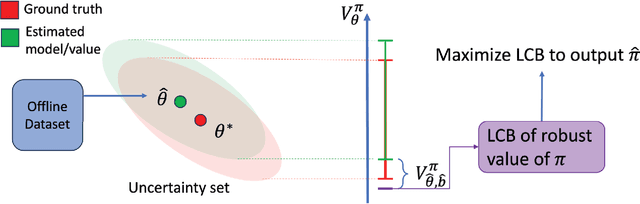

Distributionally robust offline reinforcement learning (RL) aims to find a policy that performs the best under the worst environment within an uncertainty set using an offline dataset collected from a nominal model. While recent advances in robust RL focus on Markov decision processes (MDPs), robust non-Markovian RL is limited to planning problem where the transitions in the uncertainty set are known. In this paper, we study the learning problem of robust offline non-Markovian RL. Specifically, when the nominal model admits a low-rank structure, we propose a new algorithm, featuring a novel dataset distillation and a lower confidence bound (LCB) design for robust values under different types of the uncertainty set. We also derive new dual forms for these robust values in non-Markovian RL, making our algorithm more amenable to practical implementation. By further introducing a novel type-I concentrability coefficient tailored for offline low-rank non-Markovian decision processes, we prove that our algorithm can find an $\epsilon$-optimal robust policy using $O(1/\epsilon^2)$ offline samples. Moreover, we extend our algorithm to the case when the nominal model does not have specific structure. With a new type-II concentrability coefficient, the extended algorithm also enjoys polynomial sample efficiency under all different types of the uncertainty set.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge