Robust Nonlinear Component Estimation with Tikhonov Regularization

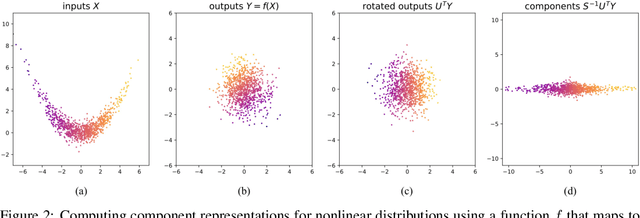
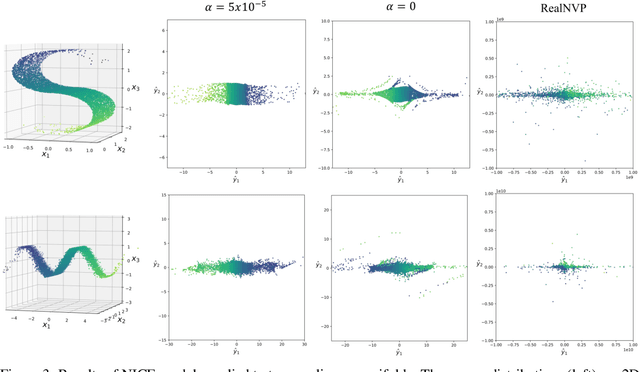
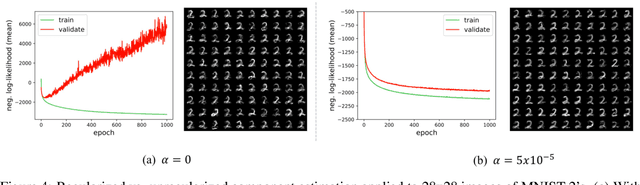
Learning reduced component representations of data using nonlinear transformations is a central problem in unsupervised learning with a rich history. Recently, a new family of algorithms based on maximum likelihood optimization with change of variables has demonstrated an impressive ability to model complex nonlinear data distributions. These algorithms learn to map from arbitrary random variables to independent components using invertible nonlinear function approximators. Despite the potential of this framework, the underlying optimization objective is ill-posed for a large class of variables, inhibiting accurate component estimates in many use cases. We present a new Tikhonov regularization technique for nonlinear independent component estimation that mediates the instability of the algorithm and facilitates robust component estimates. In addition, we provide a theoretically grounded procedure for feature extraction that produces PCA-like representations of nonlinear distributions using the learned model. We apply our technique to a handful of nonlinear data manifolds and show that the resulting representations possess important consistencies lacked by unregularized models.