Robust multirobot coordination using priority encoded homotopic constraints
Paper and Code
Aug 04, 2015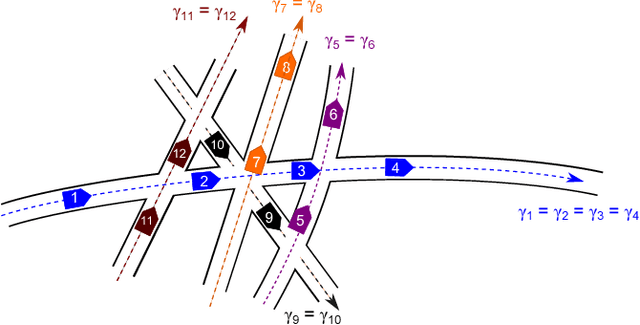
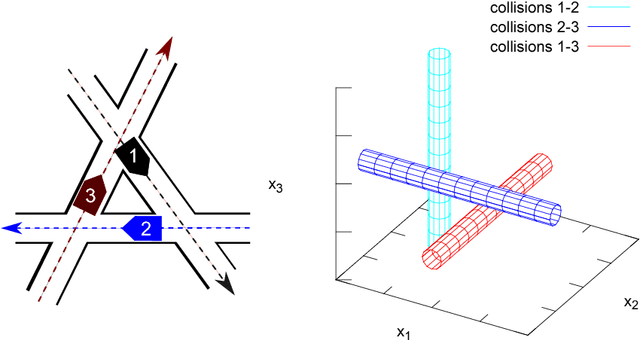
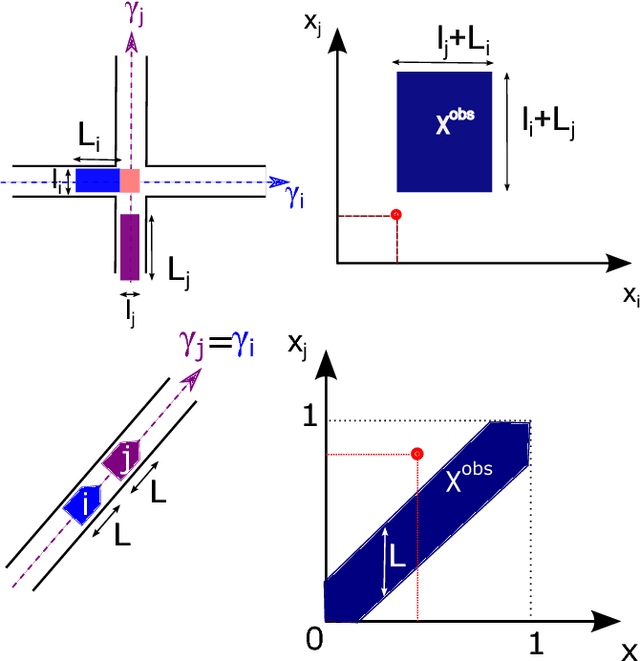
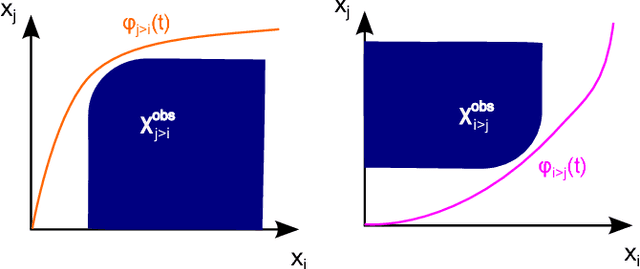
We study the problem of coordinating multiple robots along fixed geometric paths. Our contribution is threefold. First we formalize the intuitive concept of priorities as a binary relation induced by a feasible coordination solution, without excluding the case of robots following each other on the same geometric path. Then we prove that two paths in the coordination space are continuously deformable into each other if and only if they induce the \emph{same priority graph}, that is, the priority graph uniquely encodes homotopy classes of coordination solutions. Finally, we give a simple control law allowing to safely navigate into homotopy classes \emph{under kinodynamic constraints} even in the presence of unexpected events, such as a sudden robot deceleration without notice. It appears the freedom within homotopy classes allows to much deviate from any pre-planned trajectory without ever colliding nor having to re-plan the assigned priorities.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge