Robust Multi-subspace Analysis Using Novel Column L0-norm Constrained Matrix Factorization
Paper and Code
Jan 27, 2018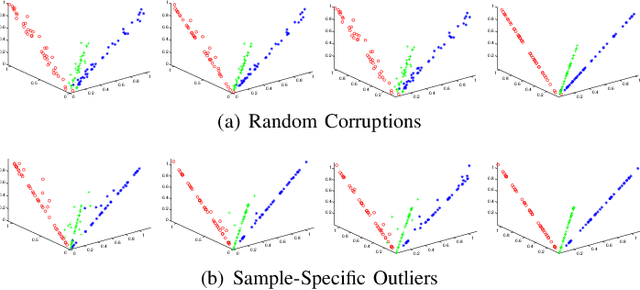

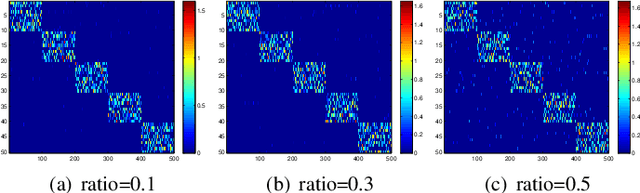
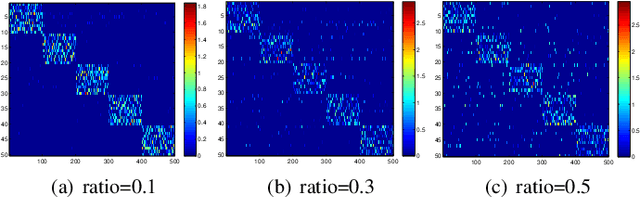
We study the underlying structure of data (approximately) generated from a union of independent subspaces. Traditional methods learn only one subspace, failing to discover the multi-subspace structure, while state-of-the-art methods analyze the multi-subspace structure using data themselves as the dictionary, which cannot offer the explicit basis to span each subspace and are sensitive to errors via an indirect representation. Additionally, they also suffer from a high computational complexity, being quadratic or cubic to the sample size. To tackle all these problems, we propose a method, called Matrix Factorization with Column L0-norm constraint (MFC0), that can simultaneously learn the basis for each subspace, generate a direct sparse representation for each data sample, as well as removing errors in the data in an efficient way. Furthermore, we develop a first-order alternating direction algorithm, whose computational complexity is linear to the sample size, to stably and effectively solve the nonconvex objective function and non- smooth l0-norm constraint of MFC0. Experimental results on both synthetic and real-world datasets demonstrate that besides the superiority over traditional and state-of-the-art methods for subspace clustering, data reconstruction, error correction, MFC0 also shows its uniqueness for multi-subspace basis learning and direct sparse representation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge