Robust Max-Product Belief Propagation
Paper and Code
Nov 27, 2011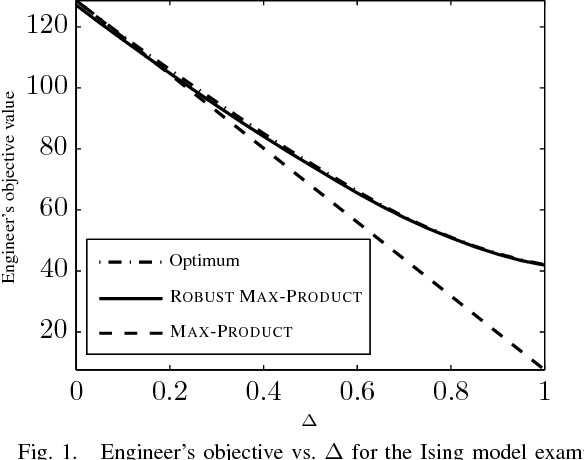
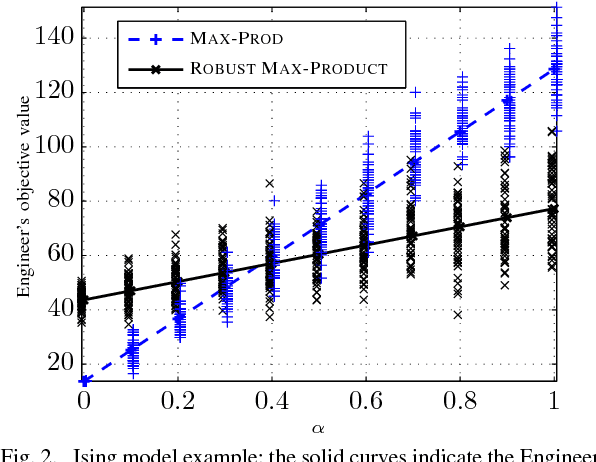
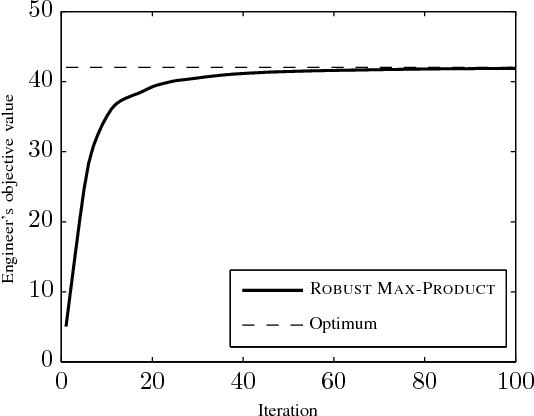
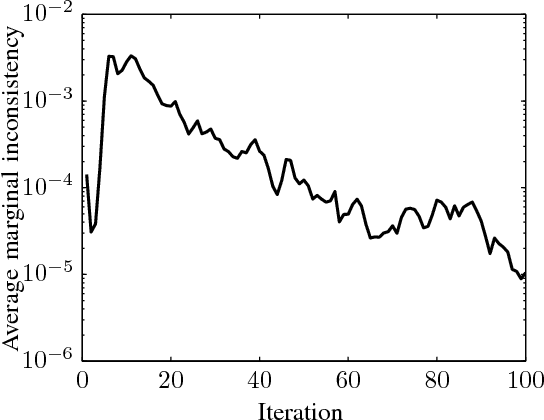
We study the problem of optimizing a graph-structured objective function under \emph{adversarial} uncertainty. This problem can be modeled as a two-persons zero-sum game between an Engineer and Nature. The Engineer controls a subset of the variables (nodes in the graph), and tries to assign their values to maximize an objective function. Nature controls the complementary subset of variables and tries to minimize the same objective. This setting encompasses estimation and optimization problems under model uncertainty, and strategic problems with a graph structure. Von Neumann's minimax theorem guarantees the existence of a (minimax) pair of randomized strategies that provide optimal robustness for each player against its adversary. We prove several structural properties of this strategy pair in the case of graph-structured payoff function. In particular, the randomized minimax strategies (distributions over variable assignments) can be chosen in such a way to satisfy the Markov property with respect to the graph. This significantly reduces the problem dimensionality. Finally we introduce a message passing algorithm to solve this minimax problem. The algorithm generalizes max-product belief propagation to this new domain.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge