Robust Forecasting for Robotic Control: A Game-Theoretic Approach
Paper and Code
Sep 22, 2022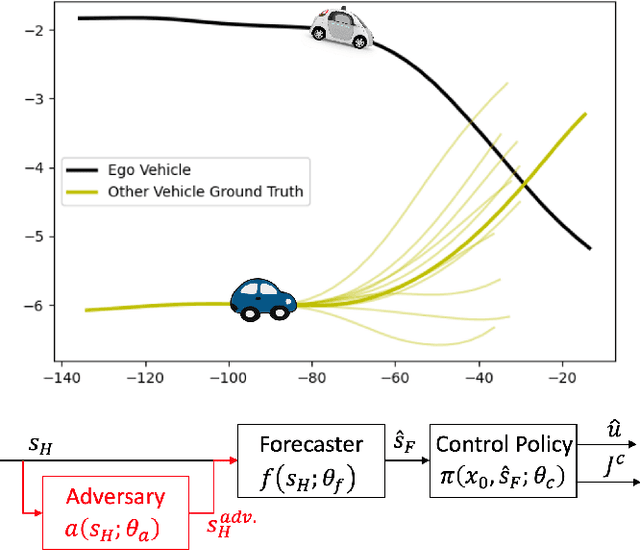
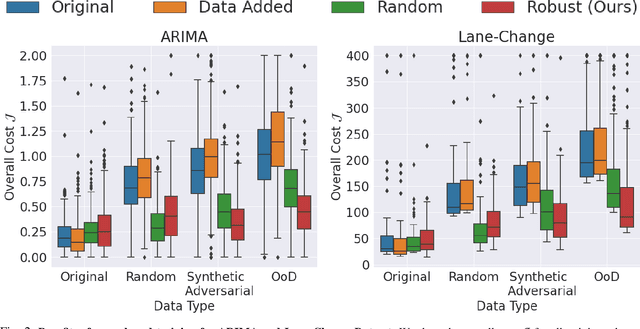
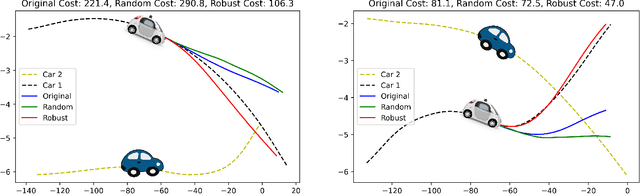
Modern robots require accurate forecasts to make optimal decisions in the real world. For example, self-driving cars need an accurate forecast of other agents' future actions to plan safe trajectories. Current methods rely heavily on historical time series to accurately predict the future. However, relying entirely on the observed history is problematic since it could be corrupted by noise, have outliers, or not completely represent all possible outcomes. To solve this problem, we propose a novel framework for generating robust forecasts for robotic control. In order to model real-world factors affecting future forecasts, we introduce the notion of an adversary, which perturbs observed historical time series to increase a robot's ultimate control cost. Specifically, we model this interaction as a zero-sum two-player game between a robot's forecaster and this hypothetical adversary. We show that our proposed game may be solved to a local Nash equilibrium using gradient-based optimization techniques. Furthermore, we show that a forecaster trained with our method performs 30.14% better on out-of-distribution real-world lane change data than baselines.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge