Robust Event-Driven Interactions in Cooperative Multi-Agent Learning
Paper and Code
Apr 07, 2022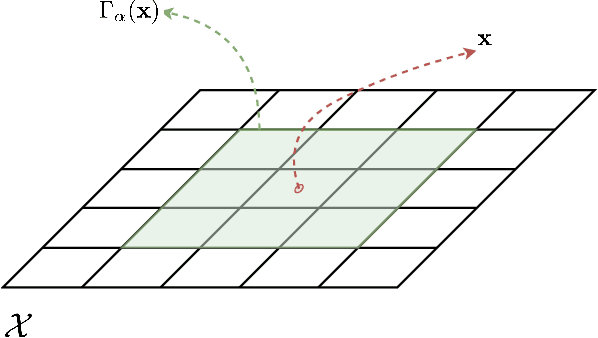
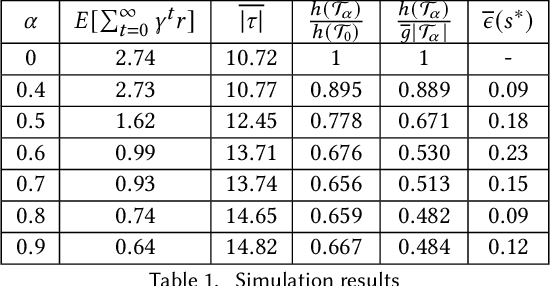
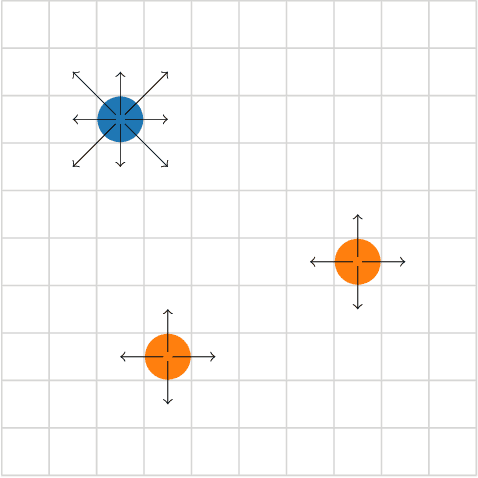
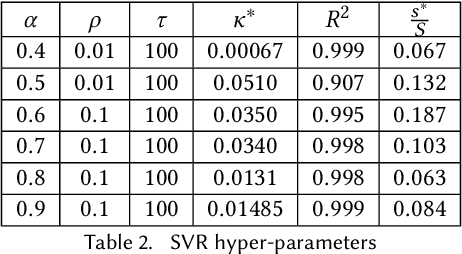
We present an approach to reduce the communication required between agents in a Multi-Agent learning system by exploiting the inherent robustness of the underlying Markov Decision Process. We compute so-called robustness surrogate functions (off-line), that give agents a conservative indication of how far their state measurements can deviate before they need to update other agents in the system. This results in fully distributed decision functions, enabling agents to decide when it is necessary to update others. We derive bounds on the optimality of the resulting systems in terms of the discounted sum of rewards obtained, and show these bounds are a function of the design parameters. Additionally, we extend the results for the case where the robustness surrogate functions are learned from data, and present experimental results demonstrating a significant reduction in communication events between agents.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge