Robotic Motion Planning using Learned Critical Sources and Local Sampling
Paper and Code
Jun 07, 2020
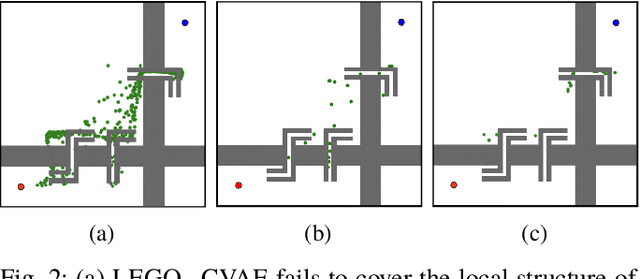
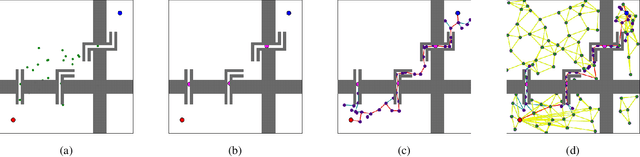
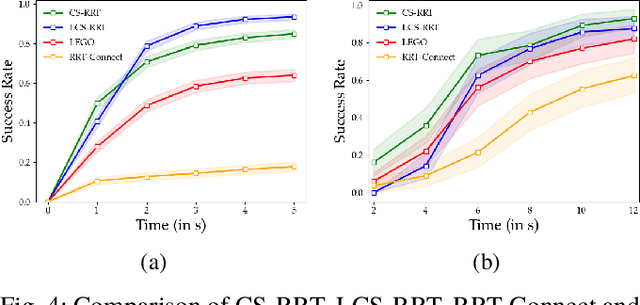
Sampling based methods are widely used for robotic motion planning. Traditionally, these samples are drawn from probabilistic ( or deterministic ) distributions to cover the state space uniformly. Despite being probabilistically complete, they fail to find a feasible path in a reasonable amount of time in constrained environments where it is essential to go through narrow passages (bottleneck regions). Current state of the art techniques train a learning model (learner) to predict samples selectively on these bottleneck regions. However, these algorithms depend completely on samples generated by this learner to navigate through the bottleneck regions. As the complexity of the planning problem increases, the amount of data and time required to make this learner robust to fine variations in the structure of the workspace becomes computationally intractable. In this work, we present (1) an efficient and robust method to use a learner to locate the bottleneck regions and (2) two algorithms that use local sampling methods to leverage the location of these bottleneck regions for efficient motion planning while maintaining probabilistic completeness. We test our algorithms on 2 dimensional planning problems and 7 dimensional robotic arm planning, and report significant gains over heuristics as well as learned baselines.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge