Risk-Sensitive Reinforcement Learning: Iterated CVaR and the Worst Path

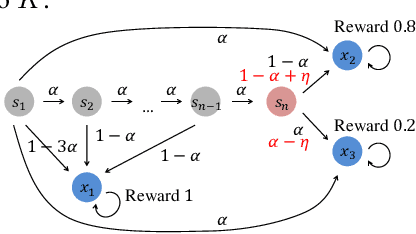
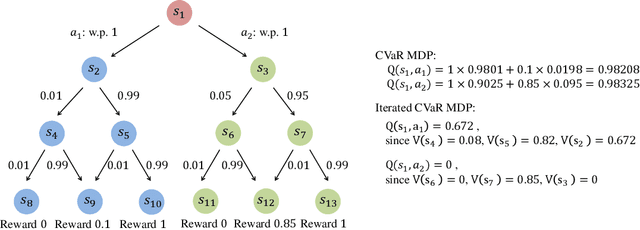
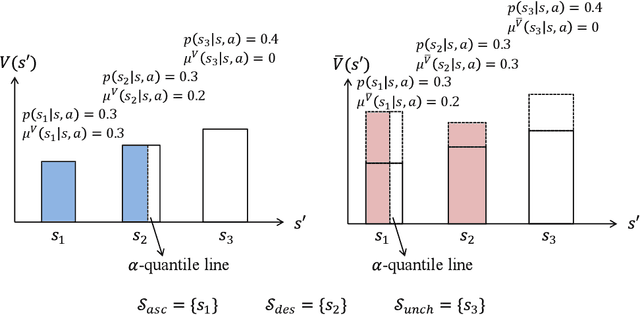
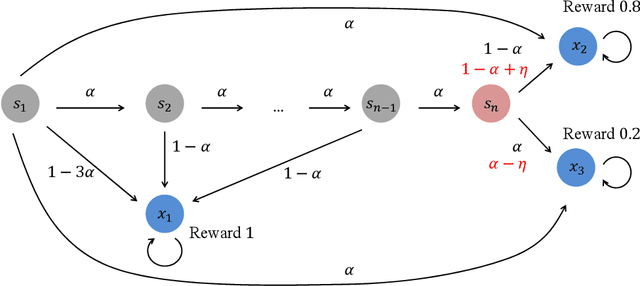
In this paper, we study a novel episodic risk-sensitive Reinforcement Learning (RL) problem, named Iterated CVaR RL, where the objective is to maximize the tail of the reward-to-go at each step. Different from existing risk-aware RL formulations, Iterated CVaR RL focuses on safety-at-all-time, by enabling the agent to tightly control the risk of getting into catastrophic situations at each stage, and is applicable to important risk-sensitive tasks that demand strong safety guarantees throughout the decision process, such as autonomous driving, clinical treatment planning and robotics. We investigate Iterated CVaR RL with two performance metrics, i.e., Regret Minimization and Best Policy Identification. For both metrics, we design efficient algorithms ICVaR-RM and ICVaR-BPI, respectively, and provide matching upper and lower bounds with respect to the number of episodes $K$. We also investigate an interesting limiting case of Iterated CVaR RL, called Worst Path RL, where the objective becomes to maximize the minimum possible cumulative reward, and propose an efficient algorithm with constant upper and lower bounds. Finally, the techniques we develop for bounding the change of CVaR due to the value function shift and decomposing the regret via a distorted visitation distribution are novel and can find applications in other risk-sensitive online learning problems.