Risk-Averse Bayes-Adaptive Reinforcement Learning
Paper and Code
Feb 10, 2021
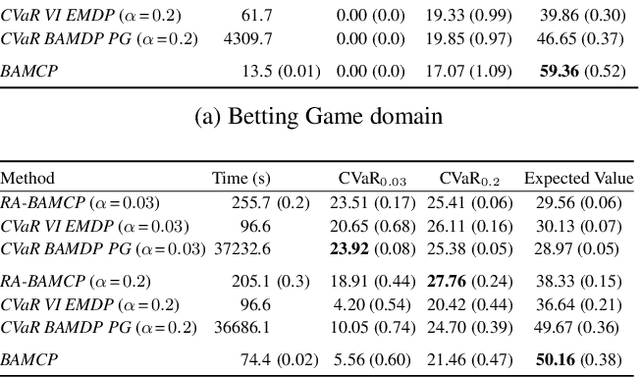
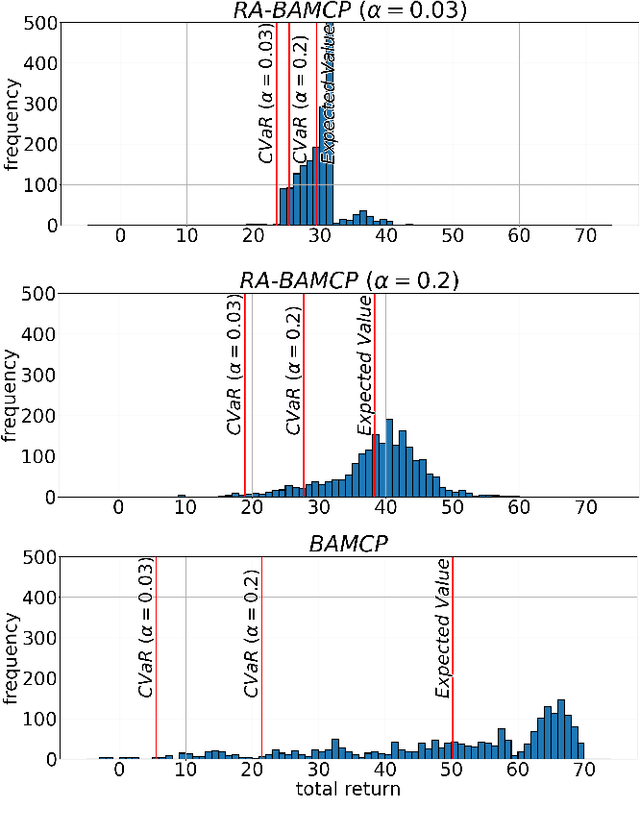

In this work, we address risk-averse Bayesadaptive reinforcement learning. We pose the problem of optimising the conditional value at risk (CVaR) of the total return in Bayes-adaptive Markov decision processes (MDPs). We show that a policy optimising CVaR in this setting is risk-averse to both the parametric uncertainty due to the prior distribution over MDPs, and the internal uncertainty due to the inherent stochasticity of MDPs. We reformulate the problem as a two-player stochastic game and propose an approximate algorithm based on Monte Carlo tree search and Bayesian optimisation. Our experiments demonstrate that our approach significantly outperforms baseline approaches for this problem.
View paper on
 OpenReview
OpenReview
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge