Rigorous data-driven computation of spectral properties of Koopman operators for dynamical systems
Paper and Code
Nov 29, 2021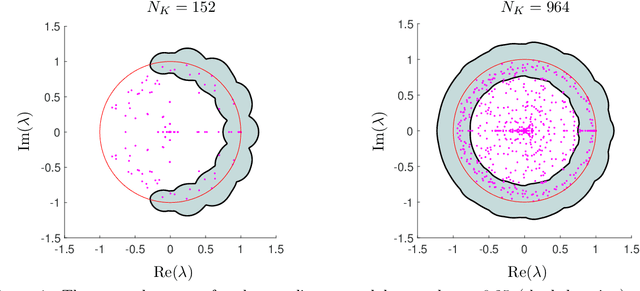
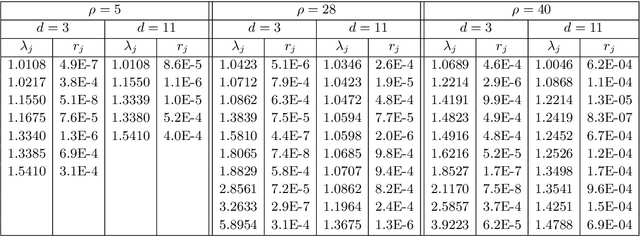
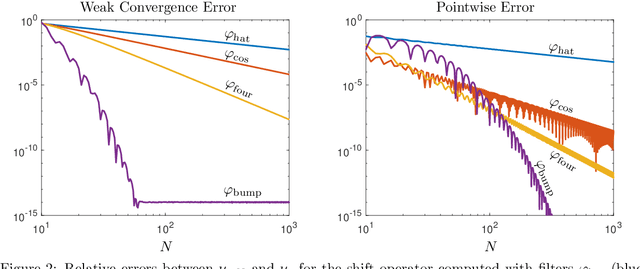

Koopman operators are infinite-dimensional operators that globally linearize nonlinear dynamical systems, making their spectral information useful for understanding dynamics. However, Koopman operators can have continuous spectra and infinite-dimensional invariant subspaces, making computing their spectral information a considerable challenge. This paper describes data-driven algorithms with rigorous convergence guarantees for computing spectral information of Koopman operators from trajectory data. We introduce residual dynamic mode decomposition (ResDMD), which provides the first scheme for computing the spectra and pseudospectra of general Koopman operators from snapshot data without spectral pollution. Using the resolvent operator and ResDMD, we also compute smoothed approximations of spectral measures associated with measure-preserving dynamical systems. We prove explicit convergence theorems for our algorithms, which can achieve high-order convergence even for chaotic systems, when computing the density of the continuous spectrum and the discrete spectrum. We demonstrate our algorithms on the tent map, Gauss iterated map, nonlinear pendulum, double pendulum, Lorenz system, and an $11$-dimensional extended Lorenz system. Finally, we provide kernelized variants of our algorithms for dynamical systems with a high-dimensional state-space. This allows us to compute the spectral measure associated with the dynamics of a protein molecule that has a 20,046-dimensional state-space, and compute nonlinear Koopman modes with error bounds for turbulent flow past aerofoils with Reynolds number $>10^5$ that has a 295,122-dimensional state-space.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge