Reward is enough for convex MDPs

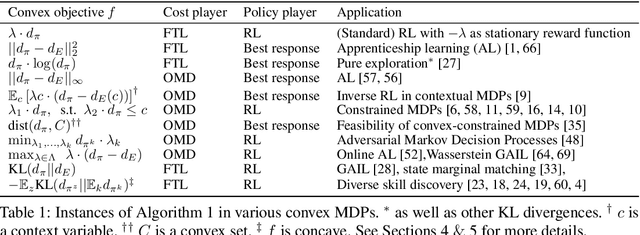
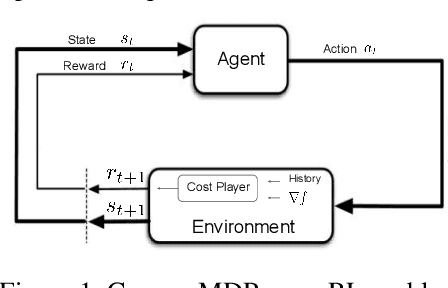
Maximising a cumulative reward function that is Markov and stationary, i.e., defined over state-action pairs and independent of time, is sufficient to capture many kinds of goals in a Markov Decision Process (MDP) based on the Reinforcement Learning (RL) problem formulation. However, not all goals can be captured in this manner. Specifically, it is easy to see that Convex MDPs in which goals are expressed as convex functions of stationary distributions cannot, in general, be formulated in this manner. In this paper, we reformulate the convex MDP problem as a min-max game between the policy and cost (negative reward) players using Fenchel duality and propose a meta-algorithm for solving it. We show that the average of the policies produced by an RL agent that maximizes the non-stationary reward produced by the cost player converges to an optimal solution to the convex MDP. Finally, we show that the meta-algorithm unifies several disparate branches of reinforcement learning algorithms in the literature, such as apprenticeship learning, variational intrinsic control, constrained MDPs, and pure exploration into a single framework.