Revisiting the Continuity of Rotation Representations in Neural Networks
Paper and Code
Jun 12, 2020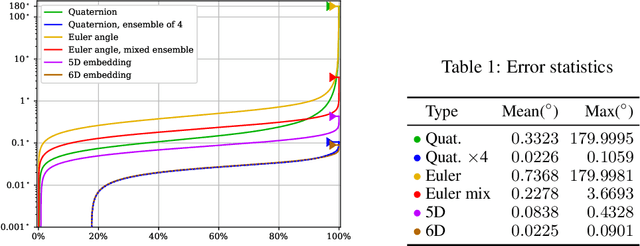
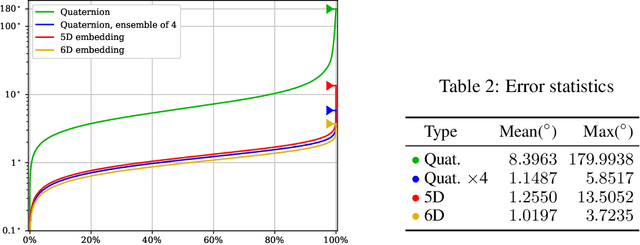
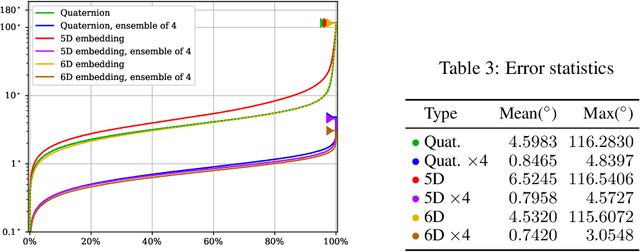
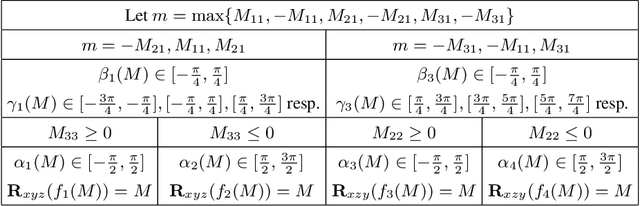
In this paper, we provide some careful analysis of certain pathological behavior of Euler angles and unit quaternions encountered in previous works related to rotation representation in neural networks. In particular, we show that for certain problems, these two representations will provably produce completely wrong results for some inputs, and that this behavior is inherent in the topological property of the problem itself and is not caused by unsuitable network architectures or training procedures. We further show that previously proposed embeddings of $\mathrm{SO}(3)$ into higher dimensional Euclidean spaces aimed at fixing this behavior are not universally effective, due to possible symmetry in the input causing changes to the topology of the input space. We propose an ensemble trick as an alternative solution.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge