Revisiting the Approximate Carathéodory Problem via the Frank-Wolfe Algorithm
Paper and Code
Nov 11, 2019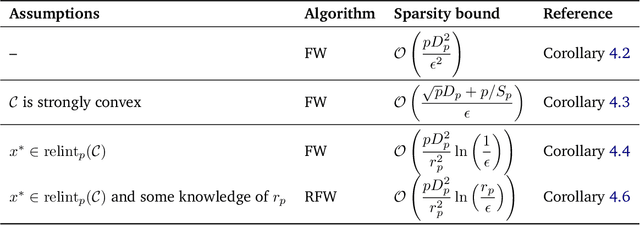
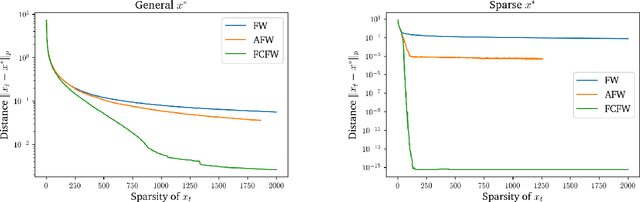
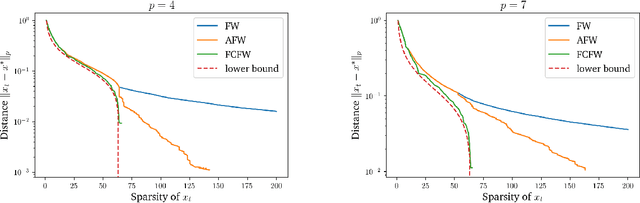
The approximate Carath\'eodory theorem states that given a polytope $\mathcal{P}$, each point in $\mathcal{P}$ can be approximated within $\epsilon$-accuracy in $\ell_p$-norm as the convex combination of $\mathcal{O}(pD_p^2/\epsilon^2)$ vertices, where $p\geq2$ and $D_p$ is the diameter of $\mathcal{P}$ in $\ell_p$-norm. A solution satisfying these properties can be built using probabilistic arguments [Barman, 2015] or by applying mirror descent to the dual problem [Mirrokni et al., 2017]. We revisit the approximate Carath\'eodory problem by solving the primal problem via the Frank-Wolfe algorithm, providing a simplified analysis and leading to an efficient practical method. Sublinear to linear sparsity bounds are derived naturally using existing convergence results of the Frank-Wolfe algorithm in different scenarios.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge