Revisiting Smoothed Online Learning
Paper and Code
Feb 13, 2021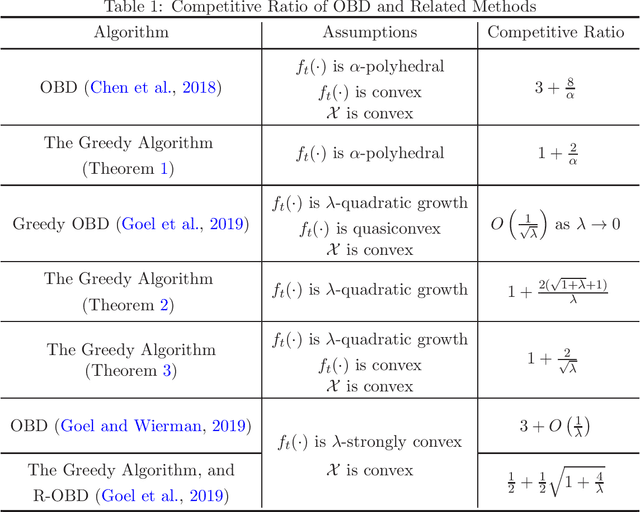

In this paper, we revisit the problem of smoothed online learning, in which the online learner suffers both a hitting cost and a switching cost, and target two performance metrics: competitive ratio and dynamic regret with switching cost. To bound the competitive ratio, we assume the hitting cost is known to the learner in each round, and investigate the greedy algorithm which simply minimizes the weighted sum of the hitting cost and the switching cost. Our theoretical analysis shows that the greedy algorithm, although straightforward, is $1+ \frac{2}{\alpha}$-competitive for $\alpha$-polyhedral functions, $1+O(\frac{1}{\lambda})$-competitive for $\lambda$-quadratic growth functions, and $1 + \frac{2}{\sqrt{\lambda}}$-competitive for convex and $\lambda$-quadratic growth functions. To bound the dynamic regret with switching cost, we follow the standard setting of online convex optimization, in which the hitting cost is convex but hidden from the learner before making predictions. We modify Ader, an existing algorithm designed for dynamic regret, slightly to take into account the switching cost when measuring the performance. The proposed algorithm, named as Smoothed Ader, attains an optimal $O(\sqrt{T(1+P_T)})$ bound for dynamic regret with switching cost, where $P_T$ is the path-length of the comparator sequence. Furthermore, if the hitting cost is accessible in the beginning of each round, we obtain a similar guarantee without the bounded gradient condition.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge