Revisiting inverse Hessian vector products for calculating influence functions
Paper and Code
Sep 25, 2024
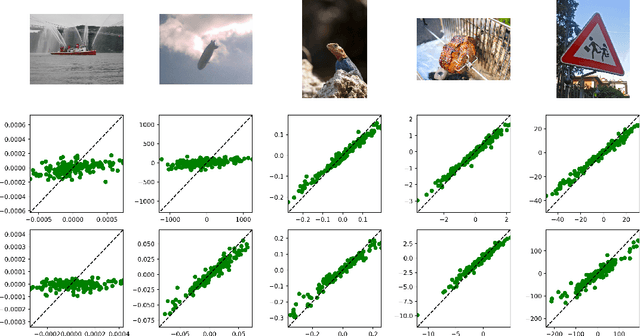
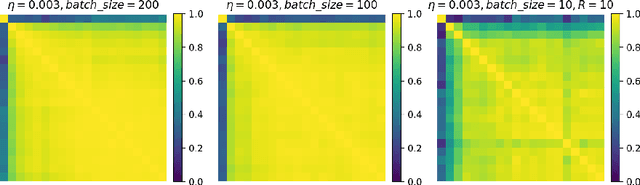

Influence functions are a popular tool for attributing a model's output to training data. The traditional approach relies on the calculation of inverse Hessian-vector products (iHVP), but the classical solver "Linear time Stochastic Second-order Algorithm" (LiSSA, Agarwal et al. (2017)) is often deemed impractical for large models due to expensive computation and hyperparameter tuning. We show that the three hyperparameters -- the scaling factor, the batch size, and the number of steps -- can be chosen depending on the spectral properties of the Hessian, particularly its trace and largest eigenvalue. By evaluating with random sketching (Swartworth and Woodruff, 2023), we find that the batch size has to be sufficiently large for LiSSA to converge; however, for all of the models we consider, the requirement is mild. We confirm our findings empirically by comparing to Proximal Bregman Retraining Functions (PBRF, Bae et al. (2022)). Finally, we discuss what role the inverse Hessian plays in calculating the influence.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge