Revealing Structure in Large Graphs: Szemerédi's Regularity Lemma and its Use in Pattern Recognition

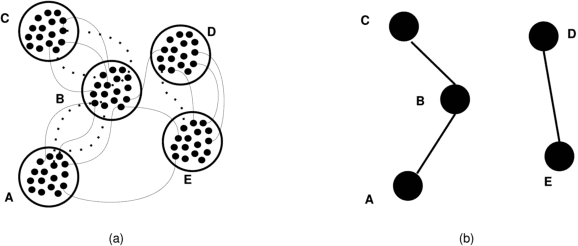
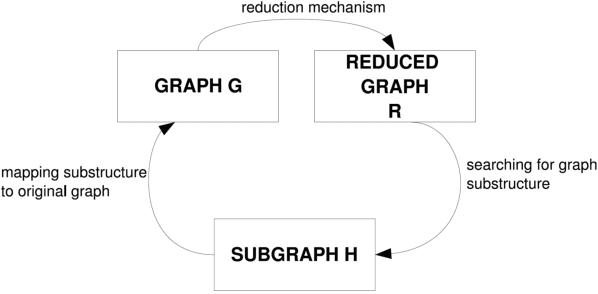
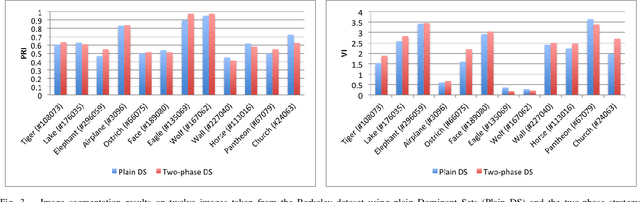
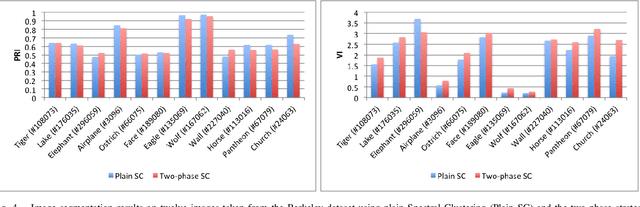
Introduced in the mid-1970's as an intermediate step in proving a long-standing conjecture on arithmetic progressions, Szemer\'edi's regularity lemma has emerged over time as a fundamental tool in different branches of graph theory, combinatorics and theoretical computer science. Roughly, it states that every graph can be approximated by the union of a small number of random-like bipartite graphs called regular pairs. In other words, the result provides us a way to obtain a good description of a large graph using a small amount of data, and can be regarded as a manifestation of the all-pervading dichotomy between structure and randomness. In this paper we will provide an overview of the regularity lemma and its algorithmic aspects, and will discuss its relevance in the context of pattern recognition research.