Rethinking WMMSE: Can Its Complexity Scale Linearly With the Number of BS Antennas?

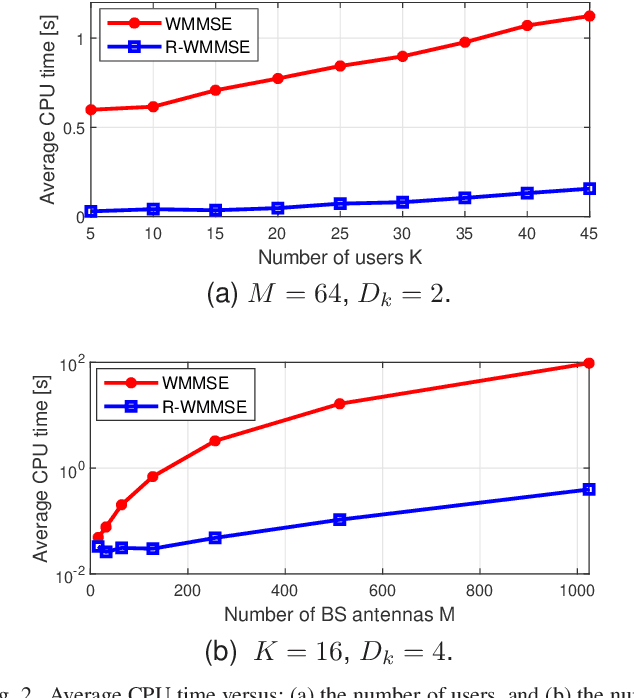
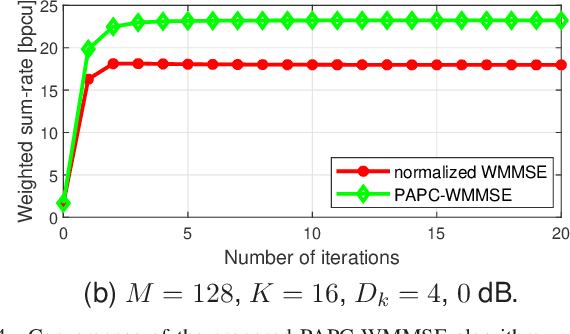
Precoding design for maximizing weighted sum-rate (WSR) is a fundamental problem for downlink of massive multi-user multiple-input multiple-output (MU-MIMO) systems. It is well-known that this problem is generally NP-hard due to the presence of multi-user interference. The weighted minimum mean-square error (WMMSE) algorithm is a popular approach for WSR maximization. However, its computational complexity is cubic in the number of base station (BS) antennas, which is unaffordable when the BS is equipped with a large antenna array. In this paper, we consider the WSR maximization problem with either a sum-power constraint (SPC) or per-antenna power constraints (PAPCs). For the former, we prove that any nontrivial stationary point must have a low-dimensional subspace structure, and then propose a reduced-WMMSE (R-WMMSE) with linear complexity by exploiting the solution structure. For the latter, we propose a linear-complexity WMMSE approach, named PAPC-WMMSE, by using a novel recursive design of the algorithm. Both R-WMMSE and PAPC-WMMSE have simple closed-form updates and guaranteed convergence to stationary points. Simulation results verify the efficacy of the proposed designs, especially the much lower complexity as compared to the state-of-the-art approaches for massive MU-MIMO systems.