Rethinking Symmetric Matrix Factorization: A More General and Better Clustering Perspective
Paper and Code
Sep 06, 2022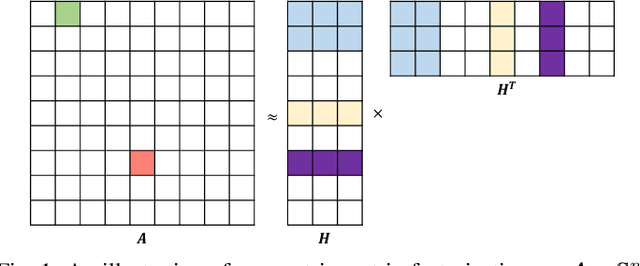
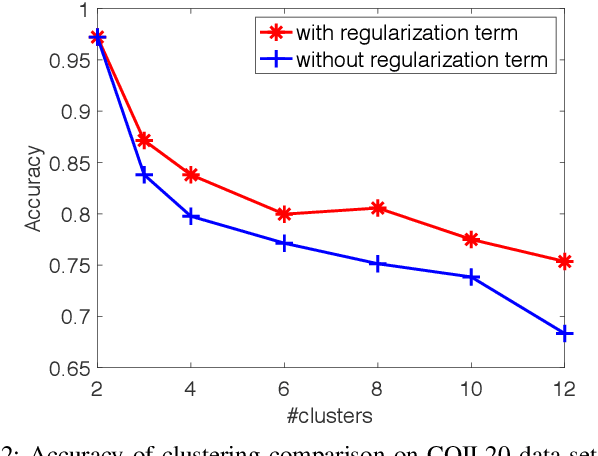
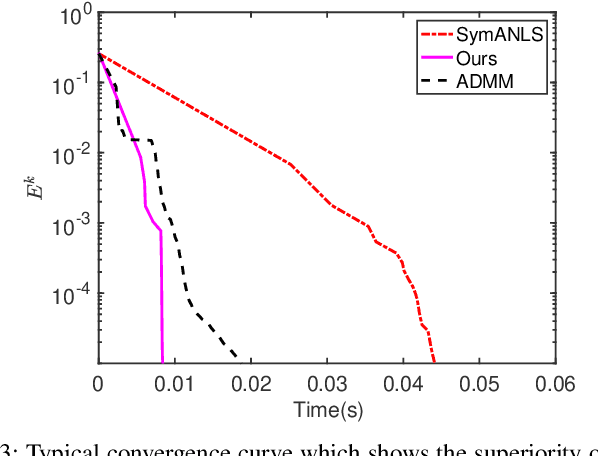
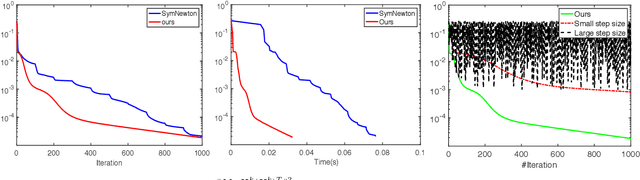
Nonnegative matrix factorization (NMF) is widely used for clustering with strong interpretability. Among general NMF problems, symmetric NMF is a special one which plays an important role for graph clustering where each element measures the similarity between data points. Most existing symmetric NMF algorithms require factor matrices to be nonnegative, and only focus on minimizing the gap between the original matrix and its approximation for clustering, without giving a consideration to other potential regularization terms which can yield better clustering. In this paper, we explore to factorize a symmetric matrix that does not have to be nonnegative, presenting an efficient factorization algorithm with a regularization term to boost the clustering performance. Moreover, a more generalized framework is proposed to solve symmetric matrix factorization problems with different constraints on the factor matrices.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge