Restrictions on Tree Adjoining Languages
Paper and Code
Oct 13, 1998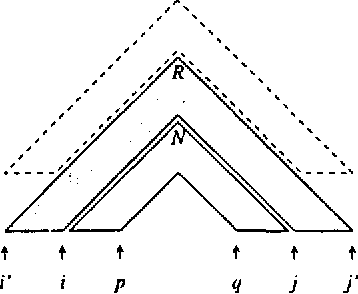
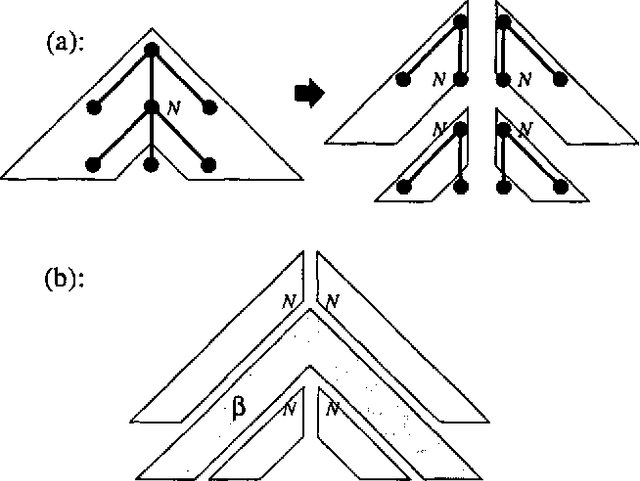
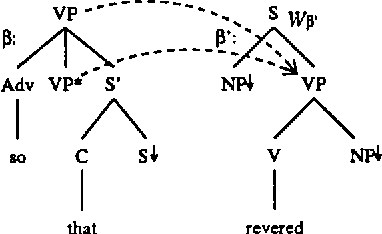

Several methods are known for parsing languages generated by Tree Adjoining Grammars (TAGs) in O(n^6) worst case running time. In this paper we investigate which restrictions on TAGs and TAG derivations are needed in order to lower this O(n^6) time complexity, without introducing large runtime constants, and without losing any of the generative power needed to capture the syntactic constructions in natural language that can be handled by unrestricted TAGs. In particular, we describe an algorithm for parsing a strict subclass of TAG in O(n^5), and attempt to show that this subclass retains enough generative power to make it useful in the general case.
* Proceedings of COLING-ACL'98 * 7 pages LaTeX + 5 eps figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge