Responsive Safety in Reinforcement Learning by PID Lagrangian Methods
Paper and Code
Jul 08, 2020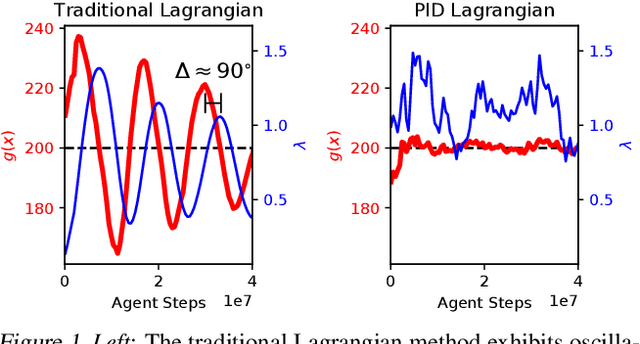
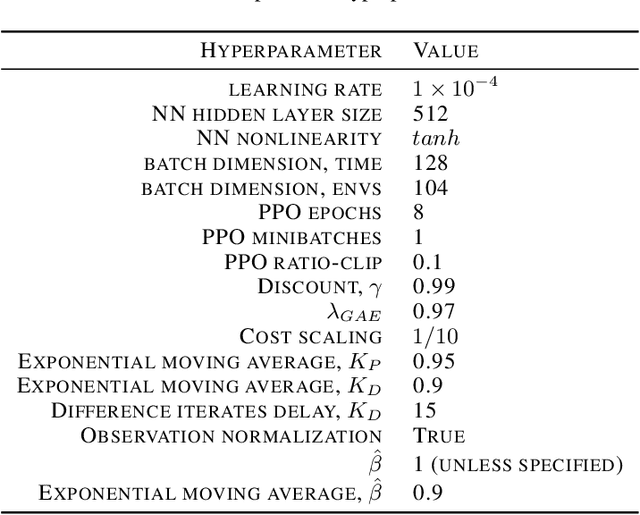
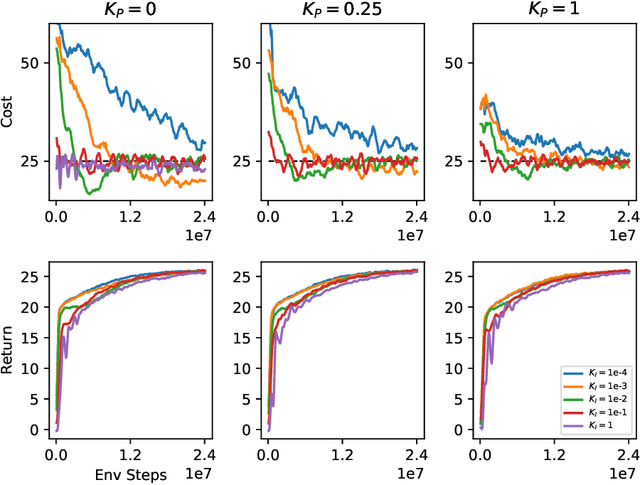

Lagrangian methods are widely used algorithms for constrained optimization problems, but their learning dynamics exhibit oscillations and overshoot which, when applied to safe reinforcement learning, leads to constraint-violating behavior during agent training. We address this shortcoming by proposing a novel Lagrange multiplier update method that utilizes derivatives of the constraint function. We take a controls perspective, wherein the traditional Lagrange multiplier update behaves as \emph{integral} control; our terms introduce \emph{proportional} and \emph{derivative} control, achieving favorable learning dynamics through damping and predictive measures. We apply our PID Lagrangian methods in deep RL, setting a new state of the art in Safety Gym, a safe RL benchmark. Lastly, we introduce a new method to ease controller tuning by providing invariance to the relative numerical scales of reward and cost. Our extensive experiments demonstrate improved performance and hyperparameter robustness, while our algorithms remain nearly as simple to derive and implement as the traditional Lagrangian approach.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge