Resolving Anomalies in the Behaviour of a Modularity Inducing Problem Domain with Distributional Fitness Evaluation
Paper and Code
Oct 15, 2021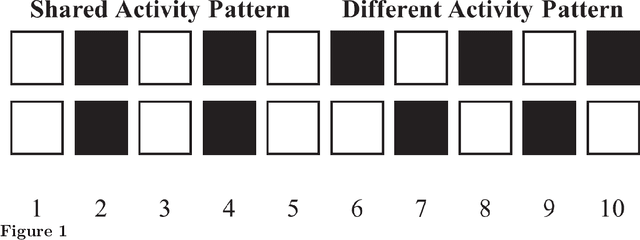

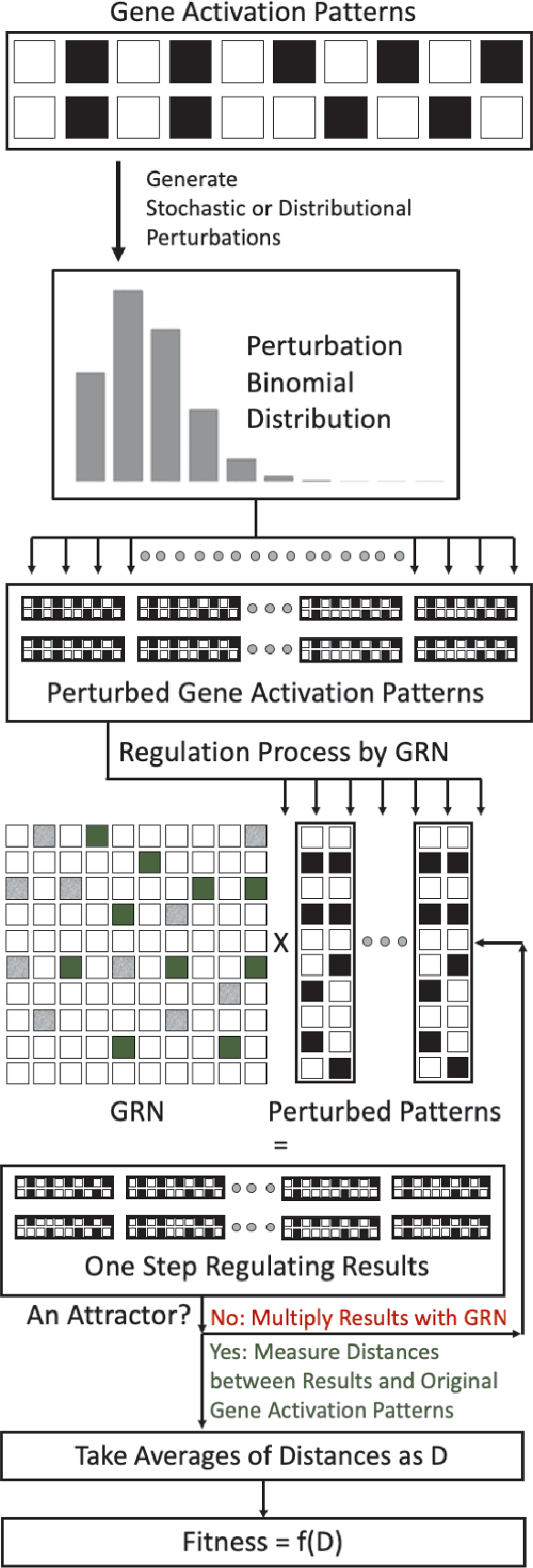

Discrete gene regulatory networks (GRNs) play a vital role in the study of robustness and modularity. A common method of evaluating the robustness of GRNs is to measure their ability to regulate a set of perturbed gene activation patterns back to their unperturbed forms. Usually, perturbations are obtained by collecting random samples produced by a predefined distribution of gene activation patterns. This sampling method introduces stochasticity, in turn inducing dynamicity. This dynamicity is imposed on top of an already complex fitness landscape. So where sampling is used, it is important to understand which effects arise from the structure of the fitness landscape, and which arise from the dynamicity imposed on it. Stochasticity of the fitness function also causes difficulties in reproducibility and in post-experimental analyses. We develop a deterministic distributional fitness evaluation by considering the complete distribution of gene activity patterns, so as to avoid stochasticity in fitness assessment. This fitness evaluation facilitates repeatability. Its determinism permits us to ascertain theoretical bounds on the fitness, and thus to identify whether the algorithm has reached a global optimum. It enables us to differentiate the effects of the problem domain from those of the noisy fitness evaluation, and thus to resolve two remaining anomalies in the behaviour of the problem domain of~\citet{espinosa2010specialization}. We also reveal some properties of solution GRNs that lead them to be robust and modular, leading to a deeper understanding of the nature of the problem domain. We conclude by discussing potential directions toward simulating and understanding the emergence of modularity in larger, more complex domains, which is key both to generating more useful modular solutions, and to understanding the ubiquity of modularity in biological systems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge