Resilient and Decentralized Control of Multi-level Cooperative Mobile Networks to Maintain Connectivity under Adversarial Environment
Paper and Code
Mar 16, 2016
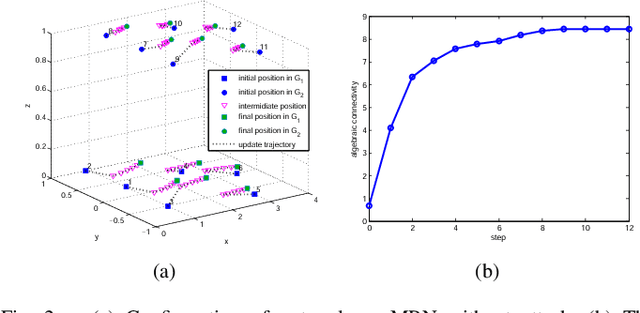
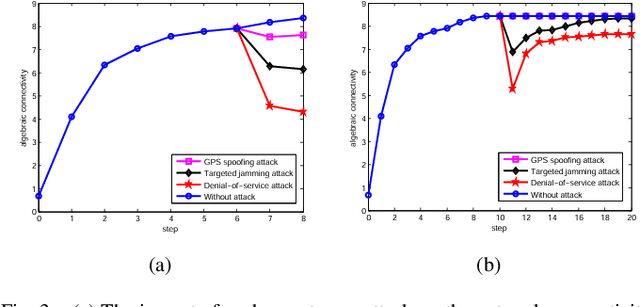
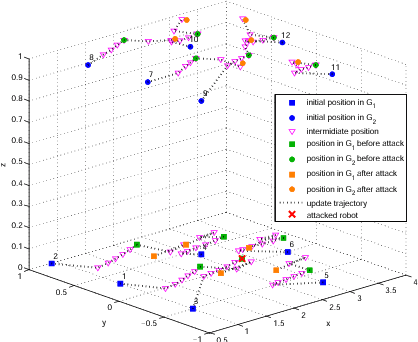
Network connectivity plays an important role in the information exchange between different agents in the multi-level networks. In this paper, we establish a game-theoretic framework to capture the uncoordinated nature of the decision-making at different layers of the multi-level networks. Specifically, we design a decentralized algorithm that aims to maximize the algebraic connectivity of the global network iteratively. In addition, we show that the designed algorithm converges to a Nash equilibrium asymptotically and yields an equilibrium network. To study the network resiliency, we introduce three adversarial attack models and characterize their worst-case impacts on the network performance. Case studies based on a two-layer mobile robotic network are used to corroborate the effectiveness and resiliency of the proposed algorithm and show the interdependency between different layers of the network during the recovery processes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge