Representing Spatial Trajectories as Distributions
Paper and Code
Oct 04, 2022
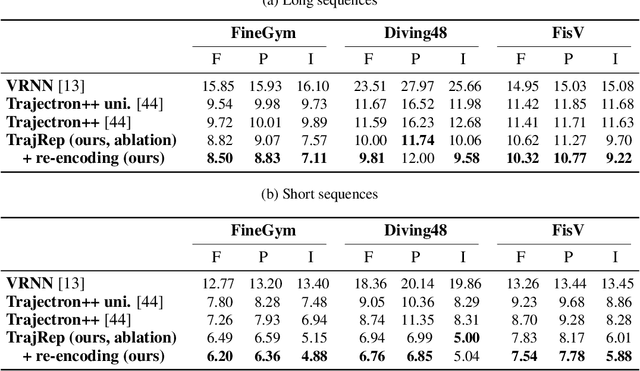
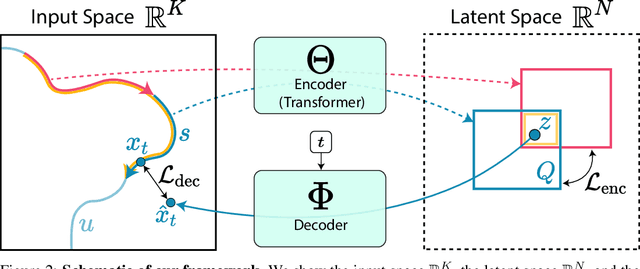
We introduce a representation learning framework for spatial trajectories. We represent partial observations of trajectories as probability distributions in a learned latent space, which characterize the uncertainty about unobserved parts of the trajectory. Our framework allows us to obtain samples from a trajectory for any continuous point in time, both interpolating and extrapolating. Our flexible approach supports directly modifying specific attributes of a trajectory, such as its pace, as well as combining different partial observations into single representations. Experiments show our method's advantage over baselines in prediction tasks.
* Accepted to NeurIPS 2022
View paper on
 OpenReview
OpenReview
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge