Representative Selection in Non Metric Datasets
Paper and Code
Jun 19, 2015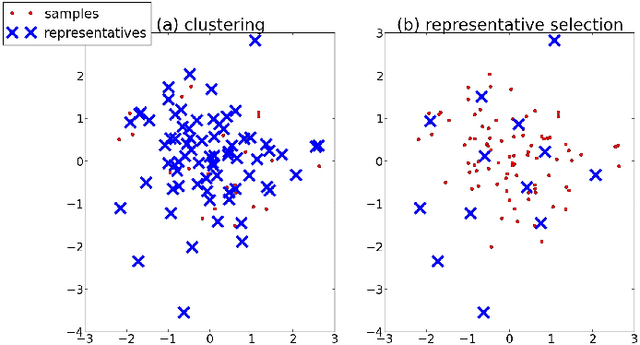
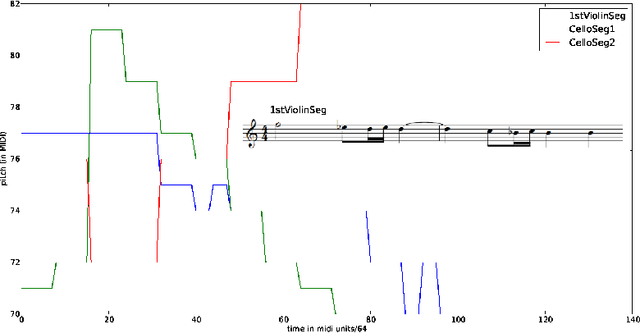
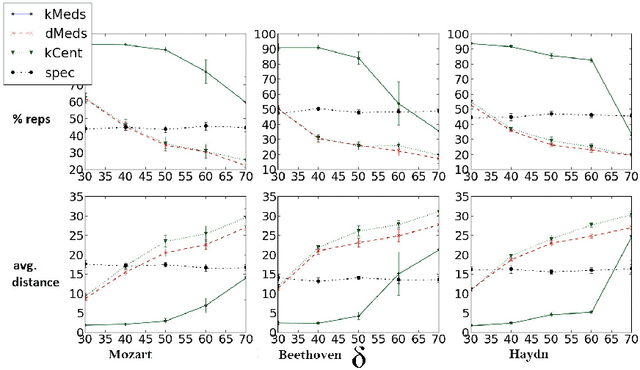
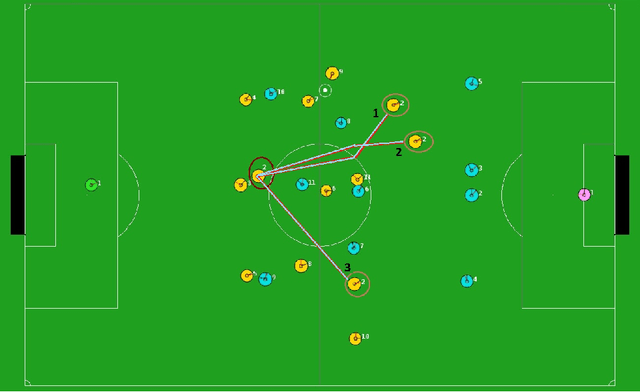
This paper considers the problem of representative selection: choosing a subset of data points from a dataset that best represents its overall set of elements. This subset needs to inherently reflect the type of information contained in the entire set, while minimizing redundancy. For such purposes, clustering may seem like a natural approach. However, existing clustering methods are not ideally suited for representative selection, especially when dealing with non-metric data, where only a pairwise similarity measure exists. In this paper we propose $\delta$-medoids, a novel approach that can be viewed as an extension to the $k$-medoids algorithm and is specifically suited for sample representative selection from non-metric data. We empirically validate $\delta$-medoids in two domains, namely music analysis and motion analysis. We also show some theoretical bounds on the performance of $\delta$-medoids and the hardness of representative selection in general.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge