Representation range needs for 16-bit neural network training
Paper and Code
Apr 06, 2021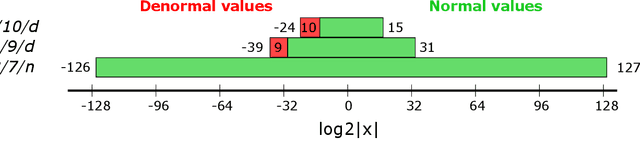

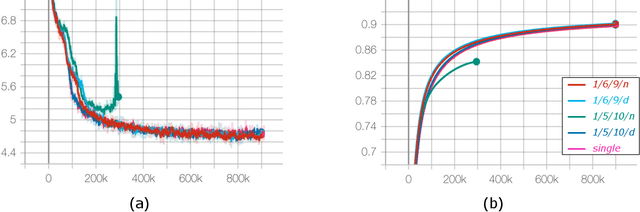

Deep learning has grown rapidly thanks to its state-of-the-art performance across a wide range of real-world applications. While neural networks have been trained using IEEE-754 binary32 arithmetic, the rapid growth of computational demands in deep learning has boosted interest in faster, low precision training. Mixed-precision training that combines IEEE-754 binary16 with IEEE-754 binary32 has been tried, and other $16$-bit formats, for example Google's bfloat16, have become popular. In floating-point arithmetic there is a tradeoff between precision and representation range as the number of exponent bits changes; denormal numbers extend the representation range. This raises questions of how much exponent range is needed, of whether there is a format between binary16 (5 exponent bits) and bfloat16 (8 exponent bits) that works better than either of them, and whether or not denormals are necessary. In the current paper we study the need for denormal numbers for mixed-precision training, and we propose a 1/6/9 format, i.e., 6-bit exponent and 9-bit explicit mantissa, that offers a better range-precision tradeoff. We show that 1/6/9 mixed-precision training is able to speed up training on hardware that incurs a performance slowdown on denormal operations or eliminates the need for denormal numbers altogether. And, for a number of fully connected and convolutional neural networks in computer vision and natural language processing, 1/6/9 achieves numerical parity to standard mixed-precision.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge