Rényi Differential Privacy of the Sampled Gaussian Mechanism

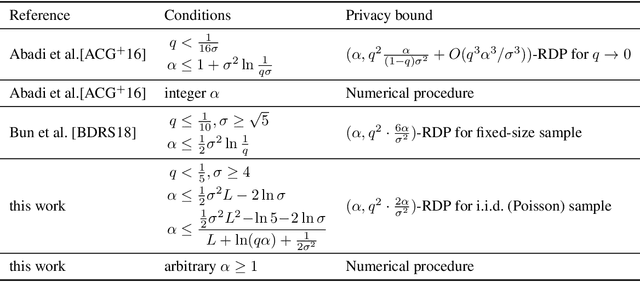
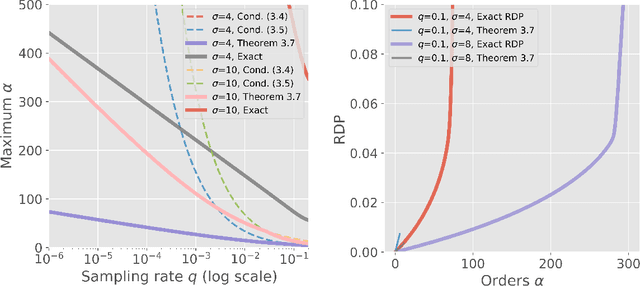
The Sampled Gaussian Mechanism (SGM)---a composition of subsampling and the additive Gaussian noise---has been successfully used in a number of machine learning applications. The mechanism's unexpected power is derived from privacy amplification by sampling where the privacy cost of a single evaluation diminishes quadratically, rather than linearly, with the sampling rate. Characterizing the precise privacy properties of SGM motivated development of several relaxations of the notion of differential privacy. This work unifies and fills in gaps in published results on SGM. We describe a numerically stable procedure for precise computation of SGM's R\'enyi Differential Privacy and prove a nearly tight (within a small constant factor) closed-form bound.