ReLU Networks as Random Functions: Their Distribution in Probability Space

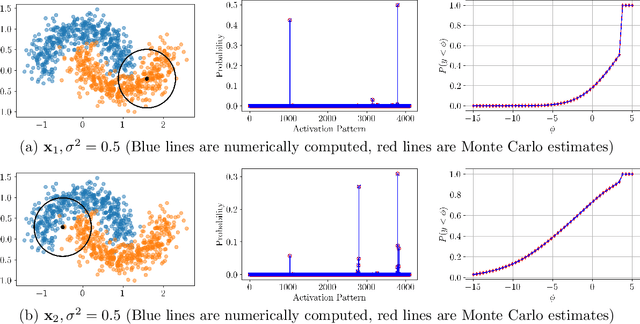
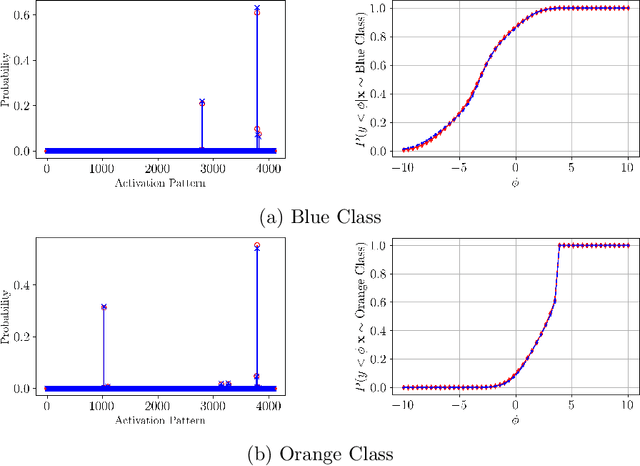
This paper presents a novel framework for understanding trained ReLU networks as random, affine functions, where the randomness is induced by the distribution over the inputs. By characterizing the probability distribution of the network's activation patterns, we derive the discrete probability distribution over the affine functions realizable by the network. We extend this analysis to describe the probability distribution of the network's outputs. Our approach provides explicit, numerically tractable expressions for these distributions in terms of Gaussian orthant probabilities. Additionally, we develop approximation techniques to identify the support of affine functions a trained ReLU network can realize for a given distribution of inputs. Our work provides a framework for understanding the behavior and performance of ReLU networks corresponding to stochastic inputs, paving the way for more interpretable and reliable models.