Relaxed Earth Mover's Distances for Chain- and Tree-connected Spaces and their use as a Loss Function in Deep Learning
Paper and Code
Nov 22, 2016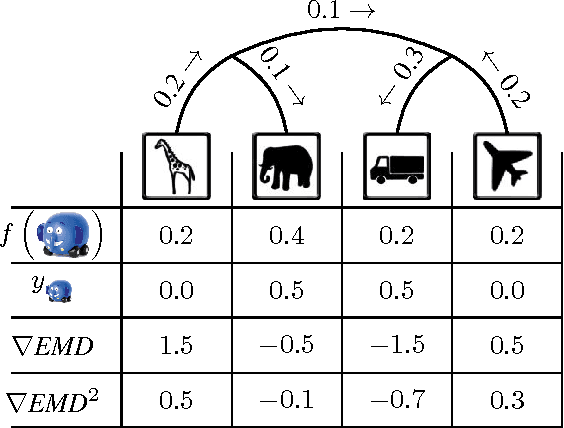

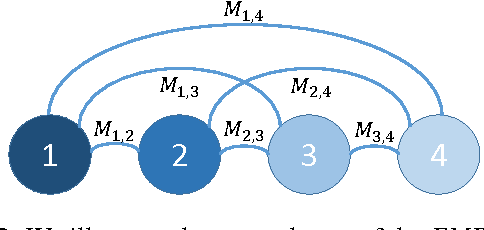
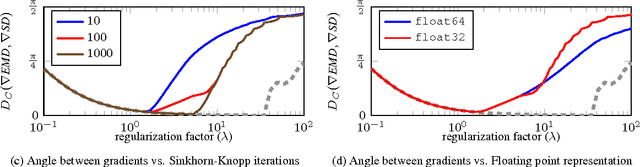
The Earth Mover's Distance (EMD) computes the optimal cost of transforming one distribution into another, given a known transport metric between them. In deep learning, the EMD loss allows us to embed information during training about the output space structure like hierarchical or semantic relations. This helps in achieving better output smoothness and generalization. However EMD is computationally expensive.Moreover, solving EMD optimization problems usually require complex techniques like lasso. These properties limit the applicability of EMD-based approaches in large scale machine learning. We address in this work the difficulties facing incorporation of EMD-based loss in deep learning frameworks. Additionally, we provide insight and novel solutions on how to integrate such loss function in training deep neural networks. Specifically, we make three main contributions: (i) we provide an in-depth analysis of the fastest state-of-the-art EMD algorithm (Sinkhorn Distance) and discuss its limitations in deep learning scenarios. (ii) we derive fast and numerically stable closed-form solutions for the EMD gradient in output spaces with chain- and tree- connectivity; and (iii) we propose a relaxed form of the EMD gradient with equivalent computational complexity but faster convergence rate. We support our claims with experiments on real datasets. In a restricted data setting on the ImageNet dataset, we train a model to classify 1000 categories using 50K images, and demonstrate that our relaxed EMD loss achieves better Top-1 accuracy than the cross entropy loss. Overall, we show that our relaxed EMD loss criterion is a powerful asset for deep learning in the small data regime.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge