Relational reasoning and generalization using non-symbolic neural networks
Paper and Code
Jun 16, 2020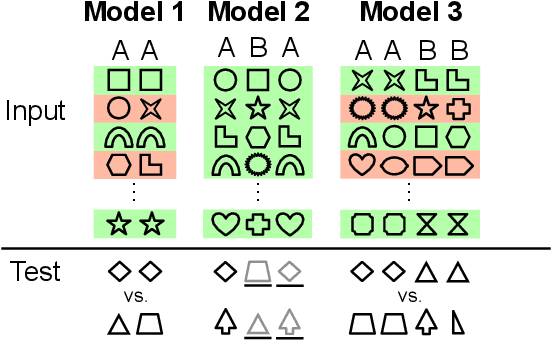
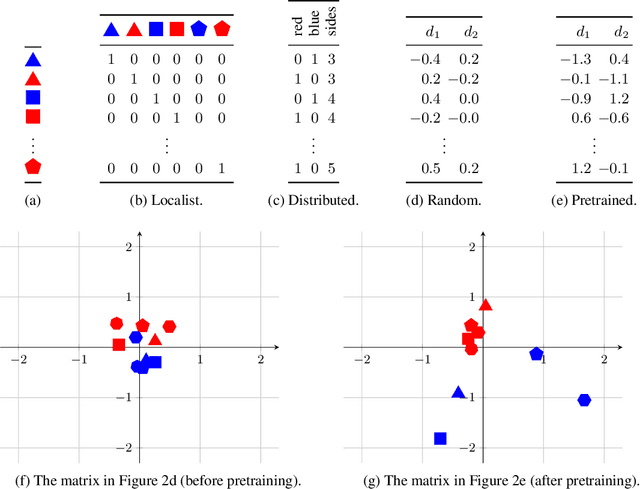
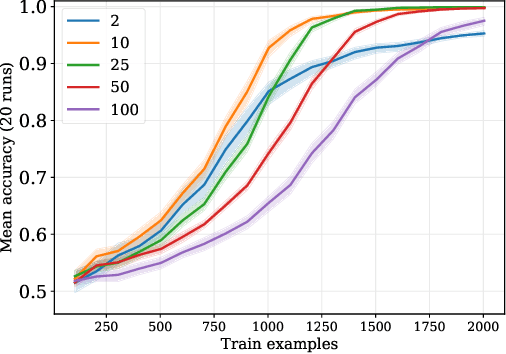
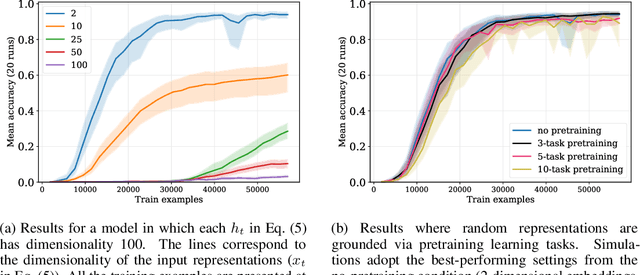
Humans have a remarkable capacity to reason about abstract relational structures, an ability that may support some of the most impressive, human-unique cognitive feats. Because equality (or identity) is a simple and ubiquitous relational operator, equality reasoning has been a key case study for the broader question of abstract relational reasoning. This paper revisits the question of whether equality can be learned by neural networks that do not encode explicit symbolic structure. Earlier work arrived at a negative answer to this question, but that result holds only for a particular class of hand-crafted feature representations. In our experiments, we assess out-of-sample generalization of equality using both arbitrary representations and representations that have been pretrained on separate tasks to imbue them with abstract structure. In this setting, even simple neural networks are able to learn basic equality with relatively little training data. In a second case study, we show that sequential equality problems (learning ABA sequences) can be solved with only positive training instances. Finally, we consider a more complex, hierarchical equality problem, but this requires vastly more data. However, using a pretrained equality network as a modular component of this larger task leads to good performance with no task-specific training. Overall, these findings indicate that neural models are able to solve equality-based reasoning tasks, suggesting that essential aspects of symbolic reasoning can emerge from data-driven, non-symbolic learning processes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge