Regularizing Neural Networks via Adversarial Model Perturbation

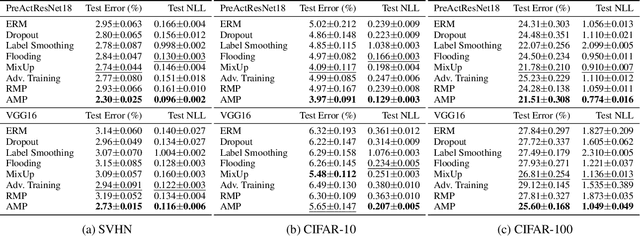
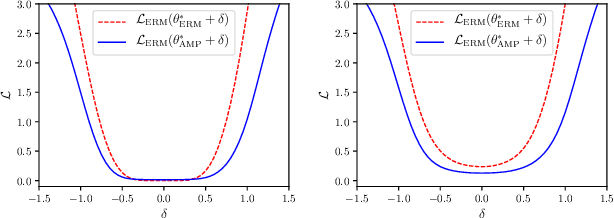
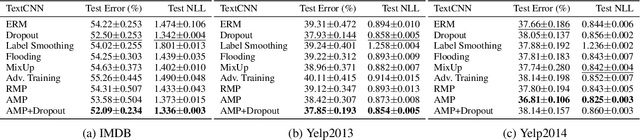
Recent research has suggested that when training neural networks, flat local minima of the empirical risk may cause the model to generalize better. Motivated by this understanding, we propose a new regularization scheme. In this scheme, referred to as adversarial model perturbation (AMP), instead directly minimizing the empirical risk, an alternative "AMP loss" function is minimized. Specifically, the AMP loss is obtained from the empirical risk by applying the "worst" norm-bounded perturbation on each point in the parameter space. We theoretically justify that minimizing the AMP loss favours flat local minima of the empirical risk and thereby improves generalization. Extensive experiments establish AMP as a new state of the art among regularization schemes.